Варианты заданий.
1. Реализовать явный и неявный метод Эйлера на равномерной сетке для решения нелинейной СОДУ и жесткой СОДУ. Реализовать метод Рунге-Кутты четвертого порядка для решения нелинейных СОДУ и исследовать возможность применения этого метода для жестких СОДУ.
2.
. Реализовать метод Рунге-Кутты второго порядка и схему с весами (схема
(2.6) с матрицей ![]() , где
, где ![]() ) для
решения нелинейных и жестких СОДУ. Исследовать влияние выбора параметра
) для
решения нелинейных и жестких СОДУ. Исследовать влияние выбора параметра ![]() на погрешность решения задачи. Решение
строить на равномерной сетке.
на погрешность решения задачи. Решение
строить на равномерной сетке.
3. Реализовать явный и неявный метод Эйлера на неравномерной сетке для решения нелинейной СОДУ и жесткой СОДУ. Реализовать метод Рунге-Кутты второго порядка для решения нелинейных СОДУ и исследовать возможность применения этого метода для жестких СОДУ.
4. Реализовать методы простого прогноза и простой коррекции на равномерной сетке для решения нелинейной СОДУ и жесткой СОДУ. Реализовать метод Рунге-Кутты четвертого порядка для решения нелинейных СОДУ и исследовать возможность применения этого метода для жестких СОДУ.
5. Реализовать методы простого прогноза и простой коррекции на неравномерной сетке для решения нелинейной СОДУ и жесткой СОДУ. Реализовать метод Рунге-Кутты второго порядка для решения нелинейных СОДУ и исследовать возможность применения этого метода для жестких СОДУ.
6. Реализовать методы двухточечного прогноза типа Милна и двухточечной коррекции типа Милна на равномерной сетке для решения нелинейной СОДУ и жесткой СОДУ. Реализовать метод Рунге-Кутты четвертого порядка для решения нелинейных СОДУ и исследовать возможность применения этого метода для жестких СОДУ.
7. Реализовать методы двухточечного прогноза типа Адамса-Башфорта и двухточечной коррекции типа Адамса-Башфорта на равномерной сетке для решения нелинейной СОДУ и жесткой СОДУ. Реализовать метод Рунге-Кутты четвертого порядка для решения нелинейных СОДУ и исследовать возможность применения этого метода для жестких СОДУ.
8. Реализовать методы двухточечного прогноза типа Милна и двухточечной коррекции типа Адамса-Башфорта на равномерной сетке для решения нелинейной СОДУ и жесткой СОДУ. Реализовать метод Рунге-Кутты четвертого порядка для решения нелинейных СОДУ и исследовать возможность применения этого метода для жестких СОДУ.
9. Реализовать методы двухточечного прогноза типа Адамса-Башфорта и двухточечной коррекции типа Милна на равномерной сетке для решения нелинейной СОДУ и жесткой СОДУ. Реализовать метод Рунге-Кутты четвертого порядка для решения нелинейных СОДУ и исследовать возможность применения этого метода для жестких СОДУ.
10. Реализовать методы трехточечного прогноза и трехточечной коррекции на равномерной сетке для решения нелинейной СОДУ и жесткой СОДУ. Реализовать метод Рунге-Кутты четвертого порядка для решения нелинейных СОДУ и исследовать возможность применения этого метода для жестких СОДУ.
Тестовые системы ОДУ.
1.
Жесткая система: 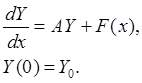
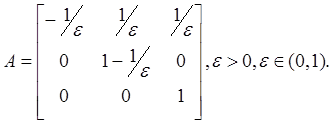
2.
Жесткая система: 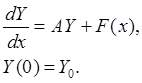
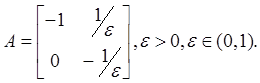
3.
Жесткая система: 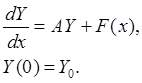
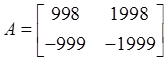 .
.
4. Нелинейная система ОДУ:
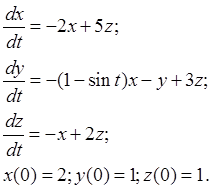
5. Нелинейная система ОДУ:
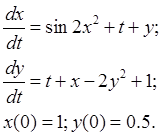
6. Нелинейная система ОДУ:
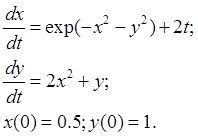
Оформление отчета.
Отчет по лабораторной работе должен включать следующие пункты.
1. Цель работы.
2. Содержание работы.
2.1. Описание метода решения СОДУ, оценка порядка аппроксимации, устойчивости и сходимости.
2.2. Описание алгоритма решения задачи.
2.3.
Анализ результатов вычислительных экспериментов. Результаты решения
модельных задач на вложенных сетках (не менее трех с шагом ![]() ), оформленные в виде таблиц и графиков.
Исследование влияния выбора шага интегрирования на точность решения жесткой
задачи.
), оформленные в виде таблиц и графиков.
Исследование влияния выбора шага интегрирования на точность решения жесткой
задачи.
2.4. Выводы.
Лабораторная работа №2. Решение краевых задач конечно-разностными методами.
Цель работы. Для краевой задачи, описывающей процесс стационарной одномерной теплопроводности, построить консервативную разностную схему, оценить порядок аппроксимации, устойчивость и сходимость.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.