Содержание работы. Пусть дано стационарное одномерное уравнение теплопроводности:
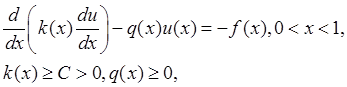
с первыми краевыми условиями:
![]()
Тогда консервативная разностная схема, т.е. схема, для которой выполняются разностные аналоги физических законов сохранения имеет вид [4]:
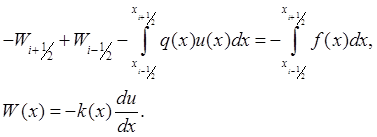
Интерполируя
значения подинтегральных функций и заменяя значение потока ![]() разностным аналогом в выражении (2.9),
получим однородную консервативную схему [4]:
разностным аналогом в выражении (2.9),
получим однородную консервативную схему [4]:
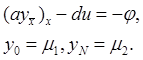
Существуют различные способы вычисления коэффициентов уравнения (2.10), например, для схемы, коэффициенты которой вычисляются путем интегрирования по интервалам сетки [4]:
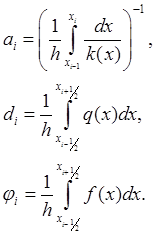
Погрешность
аппроксимации схемы (2.10) с коэффициентами (2.11) есть величина порядка ![]() при условии гладкости функций
при условии гладкости функций ![]() .
.
Полученная в результате аппроксимации краевой задачи (2.8), система линейных алгебраических уравнений (СЛАУ) имеет трехдиагональную симметричную неотрицательно определенную матрицу [4]. Для решения этой СЛАУ можно использовать либо алгоритм прогонки [4], либо уже разработанную программу решения СЛАУ с трехдиагональной матрицей (на лабораторных работах по курсу “Численные методы” [7]).
Варианты заданий.
1.
Построить консервативную схему с коэффициентами ![]() для
уравнения (2.8) с третьими и вторыми краевыми условиями.
для
уравнения (2.8) с третьими и вторыми краевыми условиями.
2. Построить консервативную схему (2.10) с коэффициентами (2.11) для уравнения (2.8) с первыми и третьими краевыми условиями.
3.
Построить консервативную схему (2.10) с коэффициентами 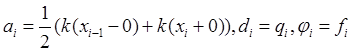 (разрывный коэффициент теплопроводности) для
уравнения (2.8) со вторыми и первыми краевыми условиями.
(разрывный коэффициент теплопроводности) для
уравнения (2.8) со вторыми и первыми краевыми условиями.
4.
Построить консервативную схему для нелинейного уравнения
теплопроводности: ![]() с коэффициентами
с коэффициентами 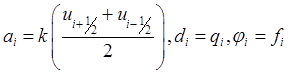 с первыми краевыми условиями.
с первыми краевыми условиями.
5.
Построить консервативную схему для нелинейного уравнения
теплопроводности: ![]() с коэффициентами
с коэффициентами ![]() с первыми краевыми условиями.
с первыми краевыми условиями.
6.
Построить консервативную схему для нелинейного уравнения
теплопроводности: ![]() с коэффициентами
с коэффициентами 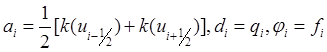 с первыми краевыми условиями.
с первыми краевыми условиями.
7.
Построить консервативную схему для нелинейного уравнения
теплопроводности: ![]() с коэффициентами
с коэффициентами 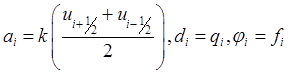 с третьими краевыми условиями.
с третьими краевыми условиями.
8.
Построить консервативную схему для нелинейного уравнения
теплопроводности: ![]() с коэффициентами
с коэффициентами ![]() с третьими краевыми условиями.
с третьими краевыми условиями.
9.
Построить консервативную схему для нелинейного уравнения теплопроводности:
![]() с коэффициентами
с коэффициентами 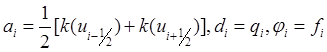 с
третьими краевыми условиями.
с
третьими краевыми условиями.
10. Построить консервативную схему для
нелинейного уравнения теплопроводности: ![]() с
коэффициентами
с
коэффициентами ![]() и сравнить со схемой с
коэффициентами
и сравнить со схемой с
коэффициентами ![]() с первыми краевыми условиями.
с первыми краевыми условиями.
Тестовые задачи.
1.
![]() Аналитическое решение уравнения (2.8):
Аналитическое решение уравнения (2.8): ![]() . Краевые условия:
. Краевые условия:
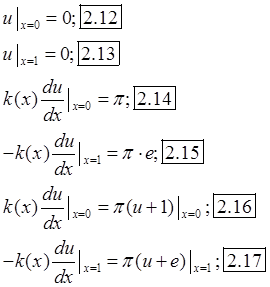
2.
![]() Аналитическое решение уравнения (2.8):
Аналитическое решение уравнения (2.8): ![]() . Краевые условия:
. Краевые условия:
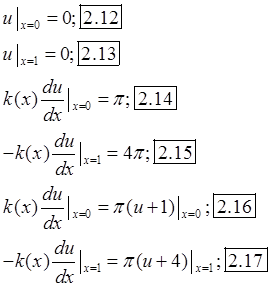
3.
![]() Аналитическое решение уравнения (2.8):
Аналитическое решение уравнения (2.8): ![]() . Краевые условия:
. Краевые условия:

4.
![]() Аналитическое решение уравнения (2.8):
Аналитическое решение уравнения (2.8): ![]() . Краевые условия:
. Краевые условия:
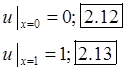
Оформление отчета.
Отчет по лабораторной работе должен включать следующие пункты.
1. Цель работы.
2. Содержание работы
2.1. Построение консервативной схемы для заданного дифференциального уравнения, оценка порядка аппроксимации, устойчивости и сходимости.
2.2. Дискретный аналог задачи (2.8). Вид СЛАУ, способ вычисления ее коэффициентов. Метод решения СЛАУ.
2.3. Описание алгоритма решения краевой задачи.
2.4.
Анализ результатов вычислительных экспериментов. Результаты тестирования
при постоянном коэффициенте теплопроводности ![]() на
вложенных сетках (не менее трех с шагом
на
вложенных сетках (не менее трех с шагом ![]() ).
Результаты тестирования с заданным коэффициентом теплопроводности
).
Результаты тестирования с заданным коэффициентом теплопроводности ![]() на вложенных сетках. Результаты оформить
в виде таблиц и графиков.
на вложенных сетках. Результаты оформить
в виде таблиц и графиков.
2.5. Выводы.
Лабораторная работа №3. Решение краевых задач методом конечных элементов.
Цель работы. Для краевой задачи, описывающей процесс стационарной одномерной теплопроводности, выписать эквивалентную вариационную постановку, построить дискретный аналог методом конечных элементов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.