В. Н. МЕДВЕДСКАЯ.Различные способы обоснования истинности предложений в начальном обучении математике//Начальная школа, 1983. - №2. – С.26-31.
Развивающее обучение предполагает систематическое и целенаправленное руководство, интеллектуальным ростом учащихся и вооружение их в процессе учения приемами и методами познавательной деятельности. Одним из средств решения поставленных задач являются доказательства.
Впервые с математическим доказательством учащиеся встречаются в курсе геометрии VI класса. Сложность мыслительной деятельности по доказыванию требует заблаговременной, длительной подготовки. Пропедевтическая работа в этом направлении может быть начата в курсе математики начальной школы. Объяснительная записка к программе этого курса ориентирует учителей на необходимость полного использования всех заложенных в нем предпосылок для формирования у детей таких приемов умственной деятельности, как сравнение, моделирование, получение выводов доказательства включаются в систему методов путем наблюдений и логических рассуждений
Для планомерного управления формированием доказывающего мышления у младших школьников учителю необходимо иметь четкие представления о сущности доказательства, о возможностях его применения в начальном обучении математике, о значении такой работы в целях подготовки учащихся к изучению математики в средней школе.
Под доказательством в логике понимают логическую операцию по обоснованию истинности одного суждения с помощью других истинных суждений. Поэтому традиционным является деление доказательства на три структурные части: 1) доказываемое суждение (тезис); 2) основание доказательства (достоверные суждения, из которых следует тезис); 3) способ доказательства (демонстрация).
В математических доказательствах основаниями для тезиса могут быть только определения, аксиомы или ранее доказанные теоремы. Основной способ таких доказательств — дедуктивный вывод. В начальной же математике, как известно, нет ни аксиом, ни теорем, да и определений немного. Значит, основания для установления истинности высказываемых суждений здесь должны быть иными.
Отбор таких оснований определяется особенностями восприятия младших школьников, уровнем их знаний, а также степенью сформированности тех или иных мыслительных операций Наглядный, конкретный характер мышления детей 7—10 лет, ограниченность их знаний ориентируют на использование в качестве критериев истины опыта, наблюдений, измерений, практики. По мере увеличения объема знаний основаниями доказательства могут служить результаты вычислений, ранее выведенные правила, свойства арифметических действий.
Анализ учебников математики для I— III классов, соответствующей им методической литературы и наблюдения уроков позволяют выделить следующие способы o6основания истинности предложений, используемых в начальном обучении математике: эксперимент, неполный индуктивный вывод, измерение, умозаключение по аналогии, дедуктивный вывод, вычисление. Назовем их способами предматематического доказательства. Приставка пред указывает на отличие такого доказательства от математического и на его роль в предварительной, предшествующей подготовке младших школьников к проведению строгих логических доказательств. Все названные способы предматематического доказательства приемов, позволяющих полнее реализовать заложенные в программе возможности интеллектуального развития учащихся. Рассмотрим каждый из них в отдельности.
1. Эксперимент — самый распространенный в начальной математике способ получения новых знаний, истинность которых устанавливается путем сопоставления их с действительностью, с результатами непосредственного чувствительного восприятия.
Экспериментально[1] доказываются предложения вида 2<3 на первых уроках по изучению нумерации чисел первого десятка, ряд свойств арифметических действий, некоторые вычислительные приемы, суждения о выборе арифметического действия для решения простых задач и т. п.
Применение этого способа предматематического доказательства начинается с создания конкретного, условного или мысленного образа рассматриваемой ситуации, построения ее модели.
Рассмотрим, например, как обосновывается истинность суждения: 2<3. В этом математическом предложении можно выделить условие: «Даны числа 2 и 3». Конкретизацией его служит построенная учителем модель: на наборном полотне выставляется 2 круга и ниже 3 квадрата. Основанием доказательства является результат непосредственного чувственного восприятия: «Один квадрат остался без пары» (рис. 1).
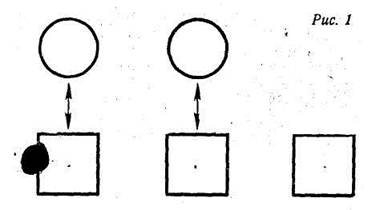
Позднее, когда на примере первых десяти чисел натурального ряда учащиеся познакомятся с принципами его построения (каждое число ряда больше всех чисел, встречающихся при счете раньше этого числа, и меньше любого числа, которое называется при счете после него), изменяются основания для доказательства предложения 2<3. И оно имеет вид: 2<3, потому что при счете число 2 называют раньше, чем число 3.
Первое — пример предматематического доказательства (экспериментального), а второе— пример дедуктивного доказательства.
Рассмотрим еще один пример экспериментального обоснования во II классе истинности распределительного свойства умножения относительно сложения (в начальной школе его называют правилом умножения суммы на число).
Учитель предлагает учащимся практическую работу: «Положите в первый ряд 4 красных и 2 зеленых круга и еще 2 таких же ряда красных и зеленых кругов. Как можно узнать, сколько всего кругов вы положили?
Для нахождения двух способов решения поставленной проблемы важную роль играет построенная учениками модель (рис. 2).
 1-й способ. Можно узнать, сколько кругов в
одном ряду (4+2). А таких рядов 3. Значит, надо сумму чисел 4 и 2 умножить на
3.
1-й способ. Можно узнать, сколько кругов в
одном ряду (4+2). А таких рядов 3. Значит, надо сумму чисел 4 и 2 умножить на
3.
2-й способ. Сначала можно найти, сколько мы положили красных кругов. Для этого надо 4 умножить на 3. Потом можно найти, сколько всего мы положили зеленых кругов. Для этого нужно 2 умножить на 3. Сложив полученные произведения, мы узнаем, сколько всего кругов мы положили.
Оба способа записываются на доске с помощью цифр и знаков арифметических действий.
Что обозначает выражение (4+2)*3?(Сколько всего кругов мы положили).
А другое выражение 4*3+2*3? (Оно тожеобозначает, сколько всего кругов мы положили.)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.