Получаемые по аналогии выводы имеют лишь правдоподобный характер. Они могут оказаться как истинными, так и ложными. К ошибкам приводит применение аналогии на частичных или несущественных при-сходства сравниваемых объектов, каждый учитель может привести конкретный пример ошибочного умозаключения по аналогии из своей практики обучения решению задач, когда, основываясь на выделении в тексте задач только отдельных слов-признаков больше, меньше, всего, осталось и т. п. (без учета их связи с другими данными задачи), учащиеся переносят известный им способ выбора арифметического действия в новые условия.
Весьма распространены у младших школьников ошибки в решении уравнений на нахождение неизвестного делимого (или уменьшаемого). Объясняются эти ошибки не столько нетвердым знанием названий этих компонентов и соответствующих правил их нахождения, сколько неправильным использованием аналогии. Решая без ошибок, к примеру, уравнения вида х*2=8 и хорошо зная правило нахождения неизвестного множителя, учащиеся переносят применяемый здесь способ решения х:=8:2 и на уравнение вида х:2 = 8. Основой для проведения аналогии служат несущественные признаки сходства этих уравнений: 1) оба уравнения с действиями одной ступени, 2) в обоих уравнениях неизвестен первый компонент. Несоответствие полученного ответа х=4 уравнению х:2 = 8 часто остается необнаруженным, поскольку к проверке уравнений многие учащиеся подходят формально, ограничиваясь только соответствующими записями (без вычислений!).
Для предупреждения ошибок подобного рода важное значение имеет установление существенных признаков отличия этих уравнений: в уравнении х*2=8 выполняется действие умножение и поэтому значение х должно быть меньше 8, а в уравнении х:2=8 — деление и значение. х должно быть больше 8.
Таким образом, правильное применение аналогии требует объема а глубины знаний существенных признаков сравниваемых объектов (как общих, так и отличительных), а также умения выделять существенные связи; между ними. Глубокое осознание к третьему году обучения общности принципов нумерации любых натуральных чисел позволяет использовать аналогию для вывода: «Письменное сложение и вычитание любых многозначных чисел выполняется так же, как сложение и вычитание трехзначных чисел» (Математика. 3, с. 37).
Можно привести немало примеров использования аналогии при изучении начального курса математики. Ее широкое применение объясняется тем, что выводы, получаемые по аналогии, позволяют систематизировать знания учащихся с наименьшими затратами сил и времени, вооружить новыми знаниями, пробудить у них интерес к математике, приобщить их к исследовательским видам деятельности. Поэтому там, где это возможно, целесообразно приобщать учащихся к самостоятельному проведению умозаключений по аналогии. Необходимым условием для этого- является предварительная актуализация знаний существенных общих и отличительных признаков сравниваемых объектов, которые создают базу для переноса знаний с одного объекта на другой.
Например, сопоставление случаев деления с
остатком на однозначное число (II класс) и на числа 10, 100, 1000 (III класс) позволяет
выделить в них существенные черты сходства (один и тот же вычислительный прием)
и различия (основой для первого является табличное или внетабличное умножение,
а для второго — нумерация натуральных чисел). По каждому из признаков у
третьеклассников имеется достаточный объем знаний, поэтому учитель может
построить урок так, чтобы учащиеся самостоятельно сделали вывод по аналогии.
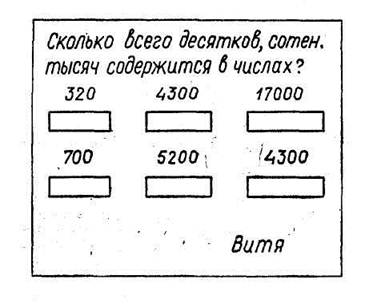
Учитель Н. И. Марцишко (школа № 21 г. Бреста) использовала эту возможность следующим образом. В устный счет она включила задания, выполнение которых актуализирует у детей необходимые для проведения аналогии знания. До начала урока учащимся были розданы перфопапки. Записав свою фамилию, ученик должен был в прорезях подчеркнуть одной чертой, сколько в соответствующем числе десятков, двумя — сколько в нем сотен, тремя — число тысяч (рис. 3).
Частичная проверка этой самостоятельной работы была выполнена после заполнения таблицы, записанной на доске (рис. 4).
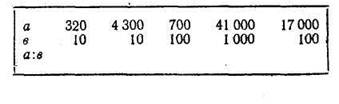Сравните частное и делимое в первой паре
примеров (второй паре, третьей паре). Что показывает частное от деления любого
числа на 10? (на 100? на 1000?)
Ответы на поставленные учителем вопросы требовали от учащихся мобилизации имеющихся у них знаний о способе нахождения частного от деления на разрядные числа.
И наконец, с полным объяснением коллективно были решены примеры 27 : 4 и 89 : 9.
Выполнение всех этих заданий явилось хорошей подготовкой для решения поставленной проблемы: «Пусть требуется 89 разделить на 10. Как это сделать?» Учащиеся быстро нашли ключ к ее решению — надо в делимом выделить наибольшее число, которое делится на 10 без остатка. Один из учеников у доски решил этот пример с полным объяснением. Для закрепления вывода, основанного на аналогии нового приема с приемом деления с остатком на однозначное число, учитель предложил сначала прочитать в учебнике объяснение деления 86 на 10, а затем прокомментировать решение примеров: 148:10; 356 : 10; 1425: 10; 24876: 10 Организованные затем наблюдения за частным и остатком в каждом примере посредством сравнения их с делимым подвели учащихся к выводу: «При делении любого числа на 10 частное показывает, сколько всего десятков в этом числе, а цифра единиц данного числа обозначает остаток». Этот вывод закреплялся путем решения примеров с окошками: 237:=23 (ост. 7); 4768: = 476 (ост. 8)
Решение новой проблемы: 4 768 : = 47 (ост. 68) опять требует от учащихся выполнения умозаключения но аналогии: «Делитель — 100, потому что частное обозначает число сотен в числе 4 768, а остаток записан всеми другими цифрами этого числа». Достоверность этого заключения учитель потребовал" доказать, предложив учащимся объяснить решение примера 4 768 : 100 и сравнить полученный ответ с ответом в примере с окошком.
Аналогия на этом уроке использовалась еще раз при отыскании приема деления на 1 000.
В течение всей работы над новым материалом учащиеся были вовлечены в творческую деятельность. Они активно участвовали в решении предлагаемых учителем познавательных задач. В ходе их решения у учащихся формировались мыслительные операции (анализ, сравнение, синтез, обобщение) и приемы умственной деятельности (наблюдение, аналогия).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.