Заданные законы движения объекта регулирования могут быть воспроизведены следящей системой лишь в том случае, если обеспечены достаточные энергетические возможности силового агрегата. Поэтому энергетический анализ объекта регулирования при его движении по заданным законам является первоочередной задачей проектирования системы.
Целью энергетического анализа является выбор элементов силового агрегата: исполнительного двигателя с редуктором и усилителя мощности.
Энергетический анализ следящей системы включает следующие основные этапы:
- анализ законов движения объектов регулирования;
- определение характера изменения и величины суммарного нагрузочного момента и мощности, потребляемой объектом регулирования;
- выбор исполнительного элемента – двигателя и анализ его перегрузочных возможностей;
- выбор передаточного числа силового редуктора;
- проверка правильности выбора исполнительного двигателя и редуктора по величине развиваемого момента и мощности.
Закон движения объекта регулирования определяется законом изменения управляющего воздействия, который может носить как детерминированный, так и случайный характер. Характер изменения управляющего воздействия определяется областью применения и целевым назначением СС.
Из всего многообразия управляющих воздействий можно выбрать ограниченное число их видов, которые с позиций анализа энергетических характеристик системы можно рассматривать как некоторые типовые обобщенные законы движения объектов регулирования. К числу типовых можно отнести движение по закону "arctg", с постоянной скоростью или постоянным ускорением, в режиме согласования (переброски).
Рассмотрим эти законы.
Движение по гармоническому закону.
В общем случае закон этого движения определяется уравнением
![]() , (3.1)
, (3.1)
где
![]() – начальный угол, относительно которого
осуществляется движение объекта регулирования по гармоническому закону;
– начальный угол, относительно которого
осуществляется движение объекта регулирования по гармоническому закону;
am – амплитуда изменения углового положения объекта регулирования;
wk – рабочая частота изменения положения объекта регулирования (частота качки).
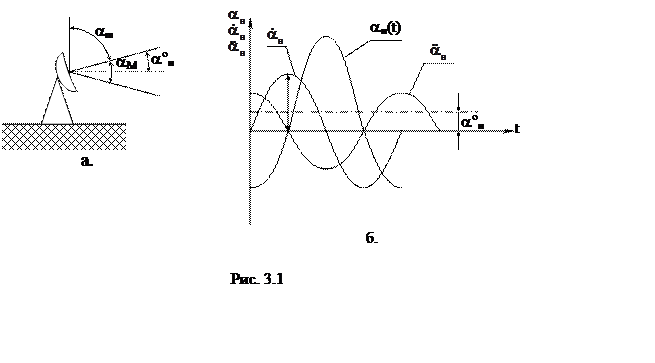 |
В практике проектирования большое распространение имеет синусоидальный закон изменения скорости объекта регулирования, для которого
![]() . (3.2)
. (3.2)
При
![]() = const
= const
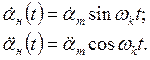
где
![]() – амплитуда скорости движения ОР;
– амплитуда скорости движения ОР;
![]() – амплитуда ускорения движения ОР.
– амплитуда ускорения движения ОР.
Графики изменения угла, скорости и ускорения движения объекта регулирования (ОР) представлены на рис. 3.1, б.
Движение по закону "arctg".
Этот тип движения характерен для следящих систем, предназначенных для сопровождения объектов наблюдения, движущихся равномерно, прямолинейно и в одной плоскости. В частности, этот закон может быть распространен на СС объектов наблюдения за спутниками или самолетами, если пренебречь кривизной земной поверхности (рис. 3.2, а). Из рисунка следует, что изменение угла aн(t) определяется зависимостью вида
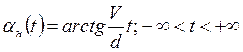 , (3.3)
, (3.3)
 |
где V – линейная скорость движения объекта наблюдения;
d – минимальная дальность до объекта наблюдения.
Дифференцируя это равенство, получим
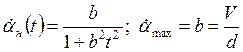 при t =
0;
при t =
0;
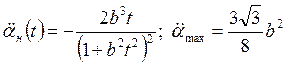 при
при 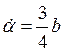 .
.
Графики изменения угла, скорости и ускорения ОР при движении по закону "arctg" показаны на рис 3.2, б.
Движение с постоянной скоростью или с постоянным ускорением.
Движение объекта регулирования этого вида имеет наиболее простой закон. Движение с постоянной скоростью характерно для следящих систем лентопротяжных механизмов, следящих систем оси часового ведения оптических телескопов, для широкого круга следящих систем, участвующих в технологических процессах, и т.д.
Для рассматриваемого закона (рис. 3.3, а)
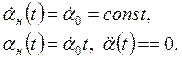
Движение с постоянным ускорением наиболее характерно для периодов разгона и торможения объекта регулирования (рис. 3.3, б).
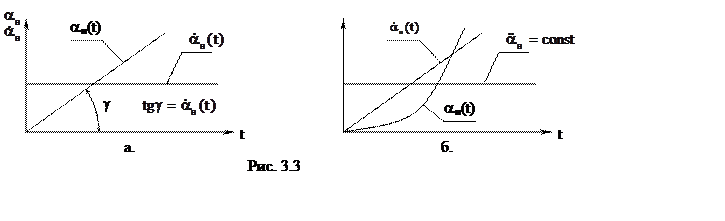 |
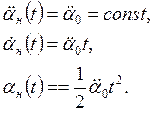
Движение объекта регулирования в режиме согласования.
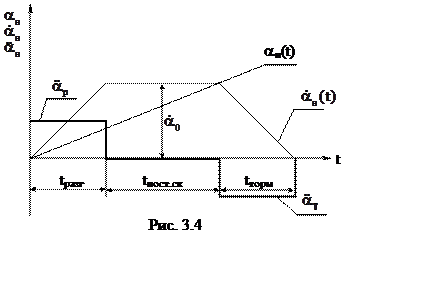
Как правило, движение объекта регулирования в режиме согласования включает в себя период разгона, период движения с постоянной скоростью и период торможения. Графики изменения угла, скорости и ускорения представлены на рис. 3.4.
 |
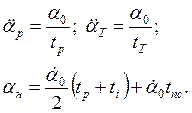
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.