На практике
 , где b=0,25¸0,6 (0,25 – для компенс. машин, 0,6 – для некомп. машин.).
, где b=0,25¸0,6 (0,25 – для компенс. машин, 0,6 – для некомп. машин.).
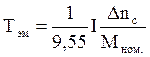 , (17)
, (17)
где 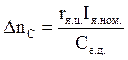 – падение скорости
двигателя в номинальном режиме.
– падение скорости
двигателя в номинальном режиме.
 ; то если
; то если ![]() , то т.к.
, то т.к. 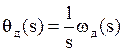 , а
, а
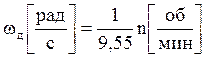 , то
, то
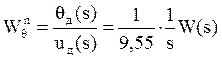 ;
;
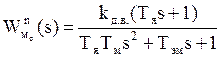 ;
;
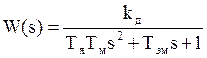 ;
;
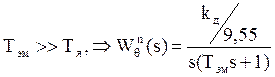 .
.
Пример:
|
Двигатель П – 22, Uном=220 В, nном=1500 об/мин, Мс=const, Iн.пр.=0,014 кгм2. Из таблицы: Uд.ном.=220 В, Iя.ном.=Iном–Iв.ном=5,64 А, Р=1, Rя.ц.=4,42 Ом, Iд=0,0138 кгм2. |
Из (4), (7), (11)
b = 0,3 (с обм. комп.). По (16)
Момент инерции на валу двигателя
|
 |
Схема двигателя изображена на рис. 3. Обмотка возбуждения ОВ питается от напряжения сети, сдвинутого на ±90о относительно напряжения на обмотке управления ОУ, для чего в ОВ вводится фазосдвигающий конденсатор Св. Для компенсации индуктивной составляющей обмотки управления обычно используется дополнительный конденсатор Су, включенный последовательно или параллельно в цепь обмотки управления. Конденсатор, как правило, подбирается так, чтобы в заторможенном двигателе получить условие резонанса в цепи управления.
Двухфазные синхронные двигатели широко используются как исполнительные элементы в маломощных следящих системах. Практическое достоинство этих двигателей заключается в том, что они не имеют коллектора и обладают высокой надежностью. В основном выпускаются двигатели двух типов: с полым немагнитным ротором из материала с хорошей электропроводностью (из алюминия) и с ферромагнитным ротором, имеющим короткозамкнутую обмотку в виде беличьей клетки. Имея меньший КПД двигатели первого типа отличаются малой инерцией ротора и лучшими регулировочными свойствами. Мощность указанных типов двигателей не превышает 100 – 200 Вт.
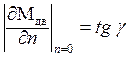 Для
механической характеристики двухфазного двигателя, обмотка управления которого
питается от источника с большой мощностью и малым внутренним сопротивлением
усилителя, характерно наличие двух видов нелинейности: нелинейность
механической характеристики Мдв=f(n) при заданном значении
напряжения управления Uу и изменение крутизны механической
характеристики
Для
механической характеристики двухфазного двигателя, обмотка управления которого
питается от источника с большой мощностью и малым внутренним сопротивлением
усилителя, характерно наличие двух видов нелинейности: нелинейность
механической характеристики Мдв=f(n) при заданном значении
напряжения управления Uу и изменение крутизны механической
характеристики
при разных значениях Uу. Последнее обстоятельство делает коэффициент усиления и постоянную времени передаточной функции двигателя переменными. Следовательно, помимо характеристик самого двигателя необходимо учитывать передаточные функции отдельных элементов системы управления.
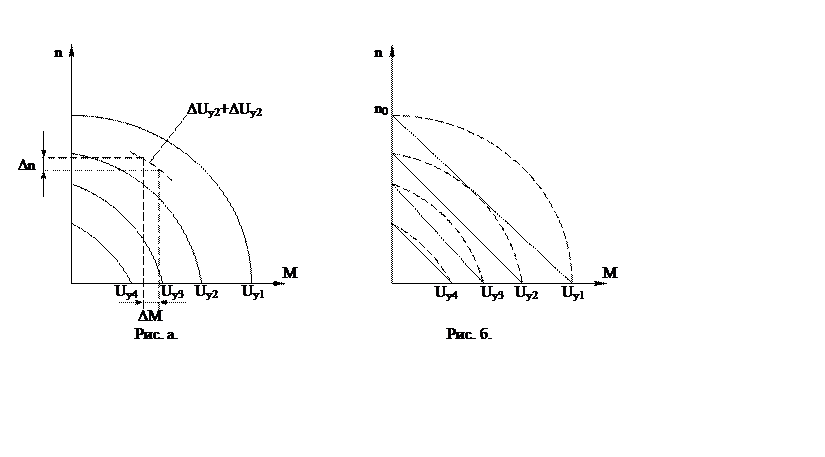
С помощью механических характеристик n=f(Uу,М)
можно найти управляющее напряжение при заданном статическом моменте
сопротивления на валу и напряжение трогания двигателя. Составим линейное
уравнение динамики двигателя в отклонениях, проведя линеаризацию его
механических характеристик. За входную величину примем напряжение на
управляющей обмотке, за выходную – угол поворота вала, полагая момент
сопротивления не зависящим от скорости вращения, что соответствует большинству
применений АД.
Механические характеристики двигателя следует линеаризовать в точке или области рабочего режима путем построения касательных к действительным характеристикам.
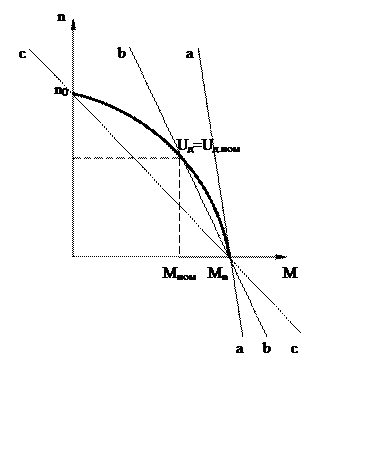 Если по форме механические характеристики близки к
линейным, то их можно заменить приближенными линейными характеристиками в виде
параллельных прямых с наклоном равным усредненному наклону прямых, соединяющих
при заданных управляющих напряжениях точки пусковых моментов и холостого хода.
Из дальнейшего рассмотрения исключим инерционность по цепи управления двигателя
ввиду ее малости. Проведя аналогию с двигателями постоянного тока при Lя=0,
на основании (6) для АД при Uв=const и малых отклонениях переменных
можно записать:
Если по форме механические характеристики близки к
линейным, то их можно заменить приближенными линейными характеристиками в виде
параллельных прямых с наклоном равным усредненному наклону прямых, соединяющих
при заданных управляющих напряжениях точки пусковых моментов и холостого хода.
Из дальнейшего рассмотрения исключим инерционность по цепи управления двигателя
ввиду ее малости. Проведя аналогию с двигателями постоянного тока при Lя=0,
на основании (6) для АД при Uв=const и малых отклонениях переменных
можно записать:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.