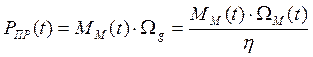Энергетический анализ объектов регулирования и выбор исполнительных элементов следящей системы, страница 3

                                                                         (3.8)

На Рис.3.5 представлены графики составляющих нагрузочного и суммарного момента при гармоническом законе движения, соответствующим уравнению (3.4) при  на валу нагрузки. По полученным графикам могут быть определены максимальные значения суммарного нагрузочного момента  и мощности, приведенные к валу двигателя. При построении графических зависимостей  и  необходимо помнить, что наличие нелинейных моментов сопротивления движению и нелинейность характеристики потерь передаваемого момента, учитываемые через к.п.д. редуктора, исключают применение метода суперпозиции для приведения к валу двигателя каждого из составляющих моментов. Необходимо предварительно просуммировать моменты, действующие со стороны объекта регулирования, после чего привести их к валу двигателя с учетом к.п.д. редуктора.

На рис.3.5б представлены диаграммы изменения моментов, действующих со стороны объекта регулирования, в режиме согласования. График изменения суммарного нагрузочного момента  показывает, что наибольшие значения момент имеет к концу участка разгона.                                                                                                                         

Для энергетического расчета и выбора параметров исполнительного двигателя важной является нагрузочная характеристика, выражающая зависимость суммарного момента нагрузки на валу органа управления или двигателя от скорости соответствующего вала.

                                                                                                           (3.9)

Вид нагрузочной характеристики зависит от требуемого закона .движения следящего вала, момента нагрузки, передаточного числа редукторов, его к.п.д.

При выборе исполнительного двигателя удобнее пользоваться диаграммой нагрузки, приведенной к валу двигателя, т.е. зависимостью требуемого момента от двигателя  от скорости его вращения

          ;     

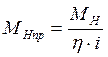Для обеспечения заданных скорости  [] и ускорения  []  двигатель должен развивать скорость  и момент , определяемые известными выражениями

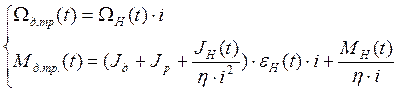                                      (3.10) , (3.11)

Система уравнений (3.10) и (3.11) является параметрическим уравнением диаграммы нагрузки. Вид диаграммы нагрузки зависит от закона движения нагрузки  и , закона изменения параметров нагрузки  и , передаточного числа i и других параметров.

Рассмотрим построение диаграммы нагрузки (нагрузочной характеристики) для случая гармонического закона движения нагрузки.

В этом случае требуемый закон движения следящего вала будет

 ,                                                          (3.12)

  ,

Для упрощения положим , . При наличии шарнирного момента, величина и знак которого определяются величиной и знаком  имеем

                                                                                                   (3.13)

С учетом указанных зависимостей уравнения (3.10) и (3.11) могут быть написаны в виде

                                                           (3.14)

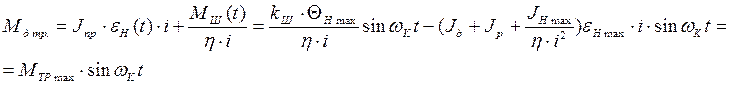(3.15)

где                                                                                         (3.16)

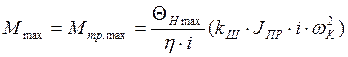                                                                (3.17)

Система уравнений (3.14) и (3.15) является уравнением эллипса. Разделив уравнение (3.14) на , а (3.15) - на , возведя полученные результаты в квадрат и сложив их, будем иметь

                                                                                   (3.18)

В данном случае нагрузочная характеристика (диаграмма нагрузки) привода представляет собой эллипс, полуоси которого определяются выражениями (3.16) и (3.17) (рис.3.6).

Как видно из этих выражений, размеры диаграммы нагрузки зависят от параметров двигателя и редуктора. При изменении передаточного числа редуктора диаграмма нагрузки деформируется.