 (1)
(1)
где 
М [Н.м] – момент двигателя,
[В.сек/рад], См [Н.м/В].
При этом уравнение моментов имеет вид:
 Се (2)
Се (2)
Решив совместно (1) и (2) и перейдя к изображениям получим уравнение АД:
(Тэмs +1)saд(s) = kдUу(s) – kд.в.Мс(s), (3)
где kд=1/Се [рад/В.с], kд.в.=1/СеСм – коэффициенты передачи двигателя по управляющему и возмущающему воздействию;
Тэм=I/СеСм [сек] – постоянная времени.
I=Iд+Iн.пр [кг.м2] – момент инерции на валу двигателя.
Постоянные Се и См могут быть найдены на основании (1) по механическим характеристикам.
При DМ=0 (М=const) получаем
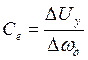 , (4)
, (4)
Dwд=0 (wд=const)
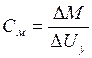 . (5)
. (5)
В случае приведения механических характеристик (рис. б)
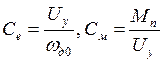 , (6)
, (6)
где wд0, Мп – скорость при холостом ходе и пусковой момент двигателя при напряжении управления Uу.
При отсутствии механических характеристик постоянные двигателя можно определить по его номинальным данным. Если механическую характеристику двигателя на рабочем участке от номинальной скорости вращения wд.ном до wд=0 при Uу=Uу.ном считать линейной, то
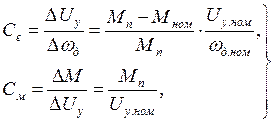 (7)
(7)
где DUу=Uу.ном–Uтр.ном,
Uтр.ном=Uу.ном.Мном/Мп – напряжение трогания при номинальном моменте.
Тогда
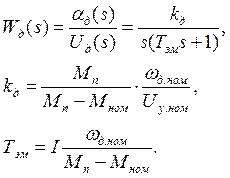
Пример:
|
Двигатель АДП – 262, Uд.ном=125 В, wд.ном=nном/9,55=194 рад/сек, Мном=49.10-3 Н.м, Iн.пр.=1,7.10-6 кгм2. Из таблицы: Мп.=49.10-3 Н.м, I=Iд+Iн.пр=3,37.10-6 кгм2. |
kд=3,5 рад/сек.В, Тэм=0,017 сек,
|
3.6.3 Сравнительная оценка САР с ПЗ и ОС
1. Чувствительность систем к изменению параметров и отклонению характеристик от линейных.
При применении ПЗ отклонения параметров и отклонение характеристик элементов от линейных сказывается на характеристиках скорректированной системы. Поэтому приходится назначать относительно жесткие требования на отклонения параметров, нестабильность и отклонение характеристик от линейных.
При ОС – нестабильность и отклонение от линейных характеристик элементов, охваченных ОС в полосе частот, где связи являются глубокими, мало сказываются на характеристиках САР. Поэтому требования здесь менее жесткие. Однако, допуски на отклонение характеристик самих ОС – жесткие, т.к. они сказываются на характеристиках САР.
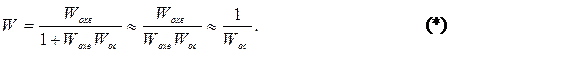 |
Желательно охватывать большее число элементов неизменяемой части системы.
2. Чувствительность к наличию нелинейности типа насыщения.
Если элемент с нелинейностью типа насыщения находится в части системы, охваченной глубокой ОС – то реакция системы на скачок входного воздействия при больших и малых отклонениях остается почти одной и той же. При больших и малых сигналах положение wср и значение запаса по фазе остаются почти неизменными. Объясняется (*).
Если вне ОС или с ПЗ коррекцией – то реакция системы на скачок малой и большой величины различна. При больших отклонениях колебания и длительность переходного процесса могут быть много больше, чем при малых отклонениях. Это объясняется тем, что для больших сигналов при выходе переменной на нелинейный участок происходит уменьшение эквивалентного коэффициента передачи элемента с насыщением, а, следовательно, и добротности. При этом wср и g уменьшаются.
Если элемент с насыщением в цепи ОС – надо чтобы линейная зона этого элемента имела достаточный запас, и чтобы входные и выходные координаты этого элемента не выходили из границ линейной зоны.
3. Чувствительность к помехам.
С ПЗ больше чем с ОС, т.к. до точки съема сигнала ОС помеха меньше (фильтр НЧ).
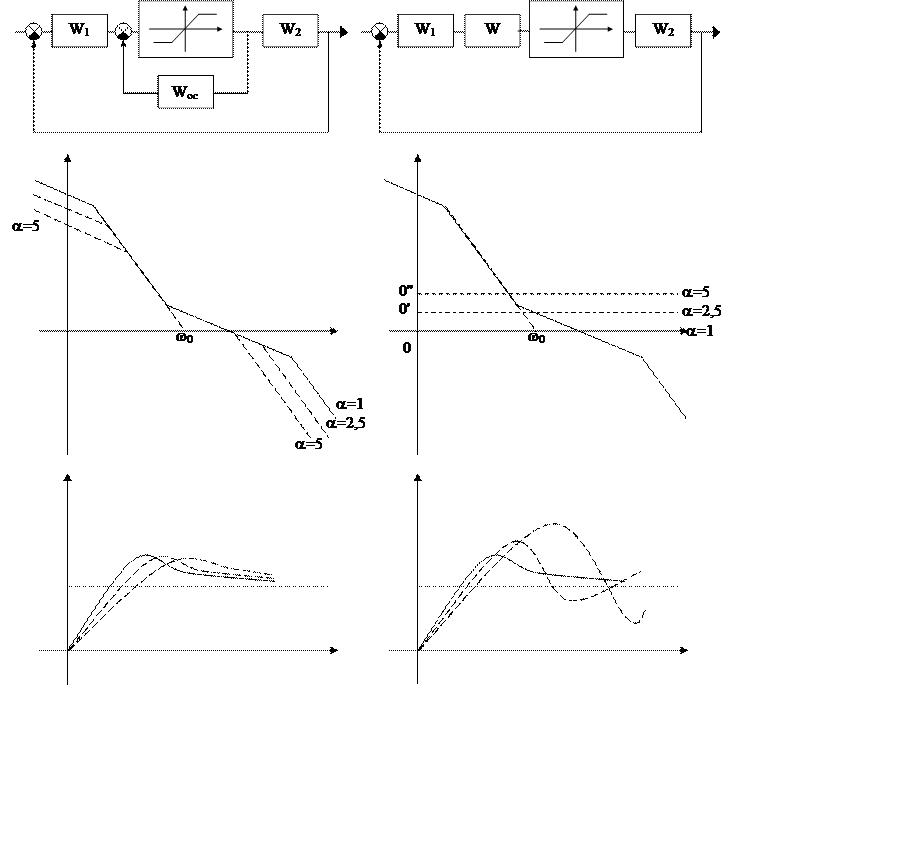
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.