Энергетический анализ объектов регулирования и выбор исполнительных элементов следящей системы, страница 12

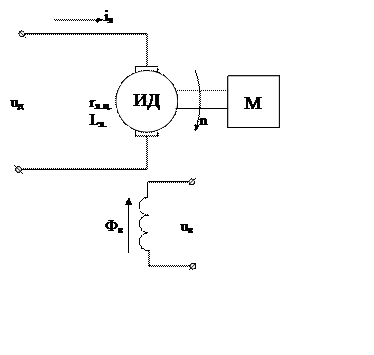
Принципиальная схема:

Статический режим работы (без учета реакции якоря).

	(1)
,	(2)
	(3)

где u_д [В]– напряжение на якоре двигателя,

i_я [A] – ток якоря,

r_я.ц. [Ом] – сопротивление цепи якоря, е_д [В]– Э.Д.С. вращения,

Ф_в [Вб] – поток возбуждения,

n [об/мин] – скорость вращения двигателя,

М [Н^.м] – момент, развиваемый двигателем.

где р – число пар полюсов,

N – число активных проводников якоря (2w_я),

А – число пар параллельных ветвей обмоток якоря.

В установившемся режиме момент двигателя уравновешивается приведенным к валу двигателя статическим моментом сопротивления нагрузки М_с, т.е.

М=Мс,	(4)
Се/См=2p/60=0,105.

Из 1 – 3 получаем уравнение механической характеристики двигателя:

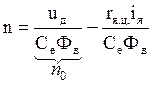 или                                                (5)

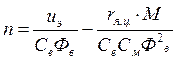.                                              (6)

В формулах (5) и (6) в правой части первый член – скорость вращения при идеальном холостом ходе (М=0, i_я=0), второй – снижение скорости вращения двигателя под нагрузкой.

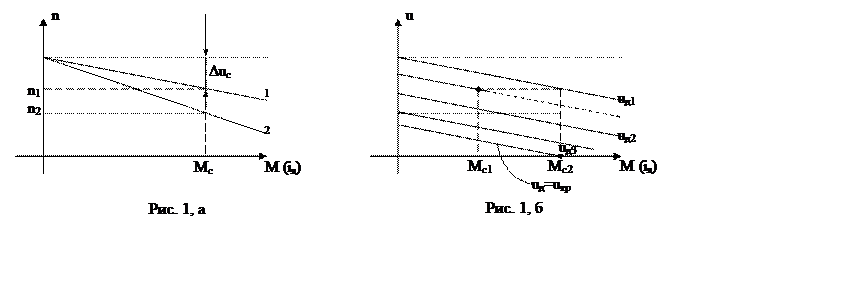
Механические характеристики при Ф_в=const и u_д=const изображены на рис.1 а). При росте сопротивления r_я.ц. жесткость механической характеристики ухудшается (2).

Конструкционные постоянные двигателя можно определить по его номинальным данным: из уравнения (5)

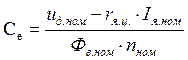 или                                     (7)

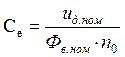,                                                                    (8)

, где  определен по механической характеристике при

Из (3):

,

,

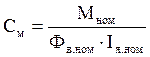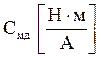;                                                               (9)

где  можно определить по механической характеристике при , или по формуле

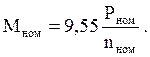                                                    (10)

где Р_ном – номинальная мощность на валу в ваттах.

(Для справки ).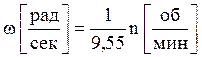

Формулы (7 – 9) используются для приближенного вычисления С_е, С_м, так как номинальные данные для двигателей усреднены.

Рассмотрим регулирование скорости вращения двигателя путем изменения напряжения на якоре.

Механические характеристики двигателя, построенные по уравнению (6) при разных напряжениях на якоре показаны на рис. 1 б). При падении напряжения механическая характеристика смещается параллельно вниз пропорционально величине напряжения. Статические характеристики позволяют определить диапазон изменения напряжения на якоре двигателя, требуемый для поддержания заданной скорости вращения при заданных пределах изменения статического момента М_с.

Соответствующие значения тока якоря можно найти используя соотношение (3). График позволяет определить зону нечувствительности двигателя, определяемую напряжением трогания (u_д=u_д.тр.). Это напряжение соответствует началу вращения двигателя и зависит от М_с. Величина u_д.тр может быть найдена также из (5) или (6) при n=0, М=М_с.

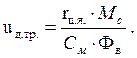
Составим уравнение динамики двигателя в отклонениях при Ф_в=const, не учитывая реакцию якоря. x_вх ® u_д, x_вых ® n. Случай, когда М_с не зависит от скорости вращения представлен на рис.

Обозначим:

С_еФ_в=С_ед, С_мФ_в=С_мд.                                               (11)

Для цепи якоря, учитывая, что е_д=С_едn из (2) при нулевых начальных условиях запишем:

U_д(s)=C_едn(s) +r_я.ц.I_я(s)+L_яsI_я(s);                                                           (12)

;        (13)

где I=I_д+I_прив =I_д+I_м /i²=I_д+k²_редI_м.

Используем зависимость (3):

M(s)=C_м.д.I_я(s).                                                         (14)

Решая совместно (12) – (14), запишем уравнение движения:

(T_яT_эмs²+T_эмs+1)n(s)=k_дu_д(s)–(T_аs+1)k_д.в.M_с(s);                (15)

где

 – постоянная времени цепи якоря,

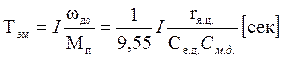 – электромеханическая постоянная  якоря,

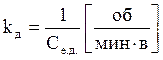 – коэффициент передачи двигателя по управляющему воздействию,

 – коэффициент передачи по возмущающему воздействию.