



























БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ "ВОЕНМЕХ"
им. Д. Ф. УСТИНОВА

КУРСОВОЙ ПРОЕКТ
по учебной дисциплине ____Проектирование СУ ЛА_______________
на тему __Алгоритм оптимального разворота ЛА на заданный угол крена
студент_______ Фомин Святослав Сегреевич _____________
Фамилия , Имя , Отчество студента группы ______И391______
 |
САНКТ-ПЕТЕРБУРГ
2014 г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ.............................................................................................................3
1. Постановка задачи..............................................................................................4
2. Разработка математической модели БПЛА......................................................4
3. Разработка алгоритма оптимального управления..........................................11
4. Алгоритм с прогнозирующей моделью...........................................................17
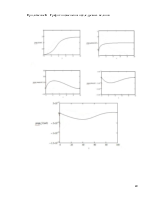
5. Результаты моделирования...............................................................................18
6. Сравнение результатов с известными решениями.........................................19
ЗАКЛЮЧЕНИЕ.....................................................................................................24
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ............................................25
Приложение А........................................................................................................26
Приложение Б........................................................................................................28
ВВЕДЕНИЕ
Объекты, с которыми имеет дело техника, органами управления. Математически поведение такого объекта описывается некоторыми уравнениями, куда входят и управляющие параметры, характеризующие положение «рулей». Естественно, возникает вопрос об отыскании наилучшего (оптимального) в том или ином смысле управления движением. Например, речь может идти о достижении цели движения за минимальное время. Этот вопрос является задачей вариационного исчисления. В отличие от классических вариационных задач, где управляющие параметры меняются в некоторой открытой области (без границы), теория оптимальное управление охватывает и тот случай, когда управляющие параметры могут принимать и граничные значения. Последнее обстоятельство особенно существенно с прикладной точки зрения, поскольку при управлении техническим объектом именно положение «руля» «на упоре» часто обеспечивает оптимальное управление.
Центральным результатом теории оптимальное управление, является принцип максимума Понтрягина, дающий общее необходимое условие оптимальности управления. Этот результат и связанные с ним исследования, проведённые Л. С. Понтрягиным и его сотрудниками, послужили исходным пунктом разработки теоретических, вычислительных и прикладных аспектов теории оптимального управления. Практически , применение теории оптимального управления является единственным способом получения преимущества при конструировании сложного многокритериального объекта при условии что все прочие возможности для обеспечении заданных параметров его функционирования уже исчерпаны . С такой ситуацией обычно приходится сталкиваться при разработке передовых образцов вооружения, когда потенциал органов управления уже достигнут за счет использования передовых промышленных технологий. Практически процесс оптимизации является итерационным. После решения задачи оптимизации по первоначальному критерию следует корректировка этого критерия с учетом возможностей практической реализации системы , отписываемой математической моделью.
1. Постановка задачи
Требуется синтез оптимального управления, при осуществлении разворота. За управляемый параметр принять угол крена. Для заданного канал управления ЛА разработать математическую модель возмущенного движения. Определить переходные характеристики переходного процесса БПЛА с оптимальным регулятором. Сравнить результаты с полученными другими методами. Отследить влияние ограничений на управляемый параметр в результатах моделирования маневра.
Известные параметры ЛА:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
V=288 м/с,
![]()
2. Разработка математической модели БПЛА
Уравнения могут быть получены из основных теорем динамики твердого тела:
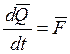 ........ , (1)
........ , (1)
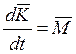 . (2)
. (2)
![]() - главный вектор и
главный момент относительно центра масс количества движения твердого тела
- главный вектор и
главный момент относительно центра масс количества движения твердого тела ![]() ;
;
![]() и
и ![]() -
главный вектор и главный момент относительно центра масс внешних сил,
действующих на твердое тело.
-
главный вектор и главный момент относительно центра масс внешних сил,
действующих на твердое тело.
Если рассматривать самолет как твердое тело в произвольный момент времени, то к нему будут приложены:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.