Алгоритм оптимального разворота ЛА на заданный угол крена, страница 7

Для задач с ограничениями используются специальные методы оптимизации, наиболее известными из которых являются принцип максимума Понтрягина и динамическое программирование Беллмана. Наиболее удобен для решения практических задач в силу своей простоты принцип максимума. Рассмотрим этот метод для задач с ограничением на управление.

Основная формулировка принципа максимума соответствует задаче обеспечения минимума функционала путем выбора оптимального управления в пределах некоторой области допустимых управлений: .

Для достижения минимума функционала (28) при заданных уравнениях объекта управления (25.1) необходимо достижение максимума функции Гамильтона по управлению

                                   (37)

при фиксированных  и , соответствующих экстремуму, и соблюдении условий трансверсальности.

Следует подчеркнуть, что речь здесь идет о достижении абсолютного экстремума.

Отметим также важную особенность, определяющую удобство применения принципа максимума: уравнение (25.11) позволяет свести задачу обеспечения минимума функционала к задаче обеспечения максимума функции Гамильтона как функции одной или нескольких переменных – составляющих вектора управления U. Предусматривается решение такой задачи для всех моментов времени в пределах рассматриваемого интервала.

Обычно область С определяется неравенствами ,  j=1,2,...,r.

Оптимальное управление на основе (25.11) может быть получено в следующих вариантах:

- как локальный экстремум внутри области C в соответствии с условиями (25.7);

- как абсолютный экстремум на границе области С ( или );

- как кусочно-непрерывная функция, на отдельных временных интервалах совпадающая с границами, а на других - принимающая значения внутри области C.

В последнем случае для точек разрыва управления (при t=t^*) следует учитывать недопустимость скачкообразного изменения переменных состояния объекта управления (условия припасовывания):

,  i=1,2,...,n;

и условия Вейерштрассе-Эрдмана:

,  i=1,2,...,n;  .

Для того что бы выяснить насколько оптимально решение по критерию Красовского , решим эту задачу с помощью принципа максимума методом Ньютона.

Решение задачи методом Ньютона включает в себя следующие шаги:

1.  Выбирается некоторое начальное приближение .

2.  Решается - система с начальными условиями , на интервале .

3.  Вычисляется вектор .

4.  В соответствии с формулой Тейлора, , откуда

5.  Определяется следующее приближение для вектора p₀: , где скалярный множитель . Выбор величины sпроисходит из требования . В качестве нормы  принимают либо , либо .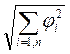

6.  Проверяется условие , i = 1, 2, …, невыполнение которого возвращает алгоритм к п.1.  Здесь - любая малая положительная величина.

Матрица  – обратная матрице частных производных .

В качестве  -системы  следует принять совместное решение систем (17) и (24).

Управление  находится из принципа максимума :

                                      (26)

В соответствии с условиями трансверсальности следует принять функцию невязок в виде(27):

                (27)

Далее, решим исходную систему данным методом, используя  те же начальные параметры что и для алгоритма с прогнозирующей моделью. :

Полученные результаты :

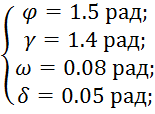
при t =3.5 сек.

В данном случае следует пояснить : как видно из алгоритма решения методом Ньютона - решается задача с правым свободным концом при предельных режимах отклонения угла крена.  Данное решение может быть принято как оптимальное по быстродействию , однако следует учесть что после совершения маневра ЛА не восстанавливает свое исходное состояние в пространстве, и продолжает движение с креном 1.4 рад.

В случае , если возникнет необходимость обеспечить исходное состояние ЛА в пространстве связанной системы координат, то можно решить эту задачу добавив в вектор конечных состояний условие  при этом решение будет выглядеть следующим образом :

при t =11.8 сек.