Алгоритм оптимального разворота ЛА на заданный угол крена, страница 3

-  рассматриваем продольное движение  БПЛА, пренебрегаем связью между продольным и боковым движением:

-  моменты инерции  БПЛА не являются функциями времени.

В силу введенных допущений получаем:

                                                           (15)

Кинематические уравнения движения центра масс  БПЛА.

Кинематические уравнения связывают между собой кинематические и геометрические характеристики поступательного движения центра масс самолёта и вращения его относительно центра масс, а также угловые скорости подвижных систем координат с параметрами движения самолёта.

Кинематическое уравнение движения центра масс  БПЛА в векторной форм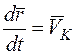е ,  где - радиус-вектор вектор скорости центра масс  БПЛА относительно рассматриваемой системы отсчета. Для получения скалярных кинематических уравнений движения центра масс найдем проекции вектора скорости  центра масс  БПЛА на оси координат, относительно которых рассматривается движение  БПЛА. Проектируя вектор скорости  на нормальные оси координат и используя таблицу направляющих косинусов, получим кинематические уравнения движения центра масс  БПЛА:

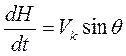                                                (16)

Кинематические уравнения, описывающие вращение  БПЛА относительно нормальной системы координат, устанавливают связь между  производными углов - по времени и проекциями на связанные оси вектора угловой скорости   БПЛА относительно системы отсчета, связанной с Землей. Поскольку вращение  БПЛА может быть представлено как изменение углов , определяющих положение  БПЛА относительно Земли, вектор угловой скорости  БПЛА   равен геометрической сумме угловых скоростей элементарных поворотов:

,                                                     

Это уравнение является кинематическим уравнением вращательного движения  БПЛА в векторной форме. Проектируя векторы  на направление связанных осей OX, OY и OZполучим:

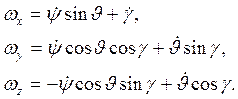
Так как  в данной работе преследуется цель демонстрации алгоритма оптимально управления , то рассматриваемая система может быть упрощена до системы в которой рассматривается только боковое движение в котором изменение траектории осуществляется только за счет угла крена , а угол крена в свою очередь регулируется рулями.  Также следует учесть что полет идет на постоянной высоте.

С учетом того, что рассматривается боковое движение  БПЛА, система дифференциальных уравнений с учетом допущений примет вид:

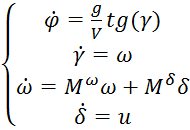                                               (17)

3. Разработка алгоритма оптимального управления

Обратимся к описанию системы управления в пространстве состояний. Модель объекта управления задается системой обыкновенных дифференциальных уравнений, возможно, нестационарной и нелинейной:

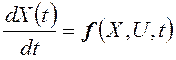,                                          (18)

где X(t)=(x₁(t),x₂(t),…,x_n(t)) – вектор состояния объекта управления, U(t)=(u₁(t),u₂(t),…,x_r(t)) – вектор управления.

С точки зрения классической теории автоматического управления, задача управляющего устройства – выработка такого управления U(t), чтобы качество функционирования системы удовлетворяло заданным требованиям (показатели точности, запаса устойчивости, быстродействия системы находились в заданных пределах). Однако эта задача может быть сформулирована и в другой форме: задача управляющего устройства – выработка такого управления, чтобы качество функционирования системы было наилучшим в определённом смысле (например, быстродействие должно быть максимальным). Такая постановка задачи имеет ряд особенностей.

1. Если не ограничиваться рассмотрением линейных стационарных систем, то в условиях задачи в общем случае необходимо оговаривать начальное X⁰=Х(t₀) и конечное состояния объекта X¹=Х(t₁). Тем самым задаётся временной интервал [t₀; t₁], для которого и требуется найти оптимальное управление. Границы этого интервала и соответствующее значение вектора X далеко не всегда оказываются фиксированными. В конкретных задачах часть из этих граничных условий может быть неизвестна или может принадлежать некоторой области. Следствием этого является разнообразие задач оптимизации управления.