Алгоритм оптимального разворота ЛА на заданный угол крена, страница 8

В данном случае длительность процесса обеспечивается общей инерционностью системы , и необходимостью фактически двойного изменения угла крена, что приводит систему в состояние , при котором на предельном управлении она движется очень ограниченное время , остальное же можно рассматривать как переходный процесс до и после такого движения.

ЗАКЛЮЧЕНИЕ

Решение задачи оптимального управления методом Красовского подходит для нахождения решения компромиссного характера для всей системы , для всей системы , и далеко не всегда обеспечивает выход на заданные режимы полета. Однако требуемого решения можно достигнуть произведя нужною балансировку свободных коэффициентов , что и было сделано в данном случае.  Компромиссное решение может оказаться полезным в условиях неопределенности дальнейших действий ЛА, так как вывод ЛА из разворота на предельных режимах может создать неблагоприятные условия для дальнейшего маневрирования.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ:

1) Кабанов С.А. Оптимизация динамики систем при действии возмущений . М: ФИЗМАТЛИТ, 2008

2) Кабанов С.А. Управление системами на прогнозирующих моделях. СПб: Издательство С-Петербургского университета, 1997

3)Е.М. Воронов Методы оптимизации управления многообъектными многокритериальными системами на основе стабильно-эффективных угровых решений. М: Издательство МГТУ им. Баумана, 2001

4)Кабанов С.А. прикладные задачи оптимального управления . СПб: БГТУ , 2007

5)Бородавкин В.А. Зверев А.И. Кабанов С.А. Санников В.А. Шалыгин А.С  Траектории. Аэродинамика. Характеристики летательных аппаратов. СПб: БГТУ , 1989

6) Лебедев А.А. Чернобровкин Л.С.   Динамика полета М: Машиностроение , 1973

ПриложениеА - Исходный код программы реализующей алгоритм с прогнозирующей моделью

t0=0

tf=10

dt=0.1

g=9.8;

v=288;

Mw=-1.8

Md=-22.4

k=0.00001;

%%

fzad=1.56;

fi(1)=0;

gamma(1)=0;

omega(1)=0;

delta(1)=0;

u(1)=0;

t=[t0:dt:tf];

%%

ro1=100;

ro2=1000;

ro3=0.01;

ro4=0.1;

%%

qfi(1)=0;

qgamma(1)=0;

qomega(1)=0;

qdelta(1)=0;

qu(1)=0;

qx(1)=0;

qz(1)=0;

tt(1)=0;

rt(1)=1;

j=1;

for t_now=1:length(t)

fi(t_now)=qfi(t_now);

gamma(t_now)=qgamma(t_now);

omega(t_now)=qomega(t_now);

delta(t_now)=qdelta(t_now);

for i=t_now:length(t)

fi(i+1)=fi(i)+dt*g/v*tan(gamma(i));

gamma(i+1)=gamma(i)+dt*omega(i);

omega(i+1)=omega(i)+dt*(Mw*omega(i)+Md*delta(i));

delta(i+1)=delta(i)+dt*u(i);

u(i+1)=u(i);

end;

p1(t_now)=ro2*(fi(length(t))-fzad);

p2(t_now)=ro1*gamma(length(t));

p3(t_now)=ro3*omega(length(t));

p4(t_now)=ro4*delta(length(t));

pp1=p1;

pp2=p2;

pp3=p3;

pp4=p4;

for i=t_now:length(t)

fi(i+1)=fi(length(t)-i+1)-dt*g/v*tan(gamma(i));

gamma(i+1)=gamma(length(t)-i+1)-dt*omega(i);

omega(i+1)=omega(length(t)-i+1)-dt*(Mw*omega(i)+Md*delta(i));

delta(i+1)=delta(length(t)-i+1)-dt*u(i);

p1(i+1)=p1(i);

p2(i+1)=p2(i)-dt*(-p1(i)*g/(v*cos(gamma(i))*cos(gamma(i))));

p3(i+1)=p3(i)-dt*(-p2(i)-p3(i)*Mw);

p4(i+1)=p4(i)-dt*(-p3(i)*Md);

end;

UU=-k*p4(length(t));

qu(t_now)=UU;

qfi(t_now+1)=qfi(t_now)+dt*g/v*tan(qgamma(t_now));

qgamma(t_now+1)=qgamma(t_now)+dt*qomega(t_now);

if qgamma(t_now+1)>1.5

qgamma(t_now+1)=1.5;

end;

qomega(t_now+1)=qomega(t_now)+dt*(Mw*qomega(t_now)+Md*qdelta(t_now));

if qomega(t_now+1)>1.45

qomega(t_now+1)=1.45;

end;

qdelta(t_now+1)=qdelta(t_now)+dt*qu(t_now);

qu(t_now+1)=qu(t_now);

qx(t_now+1)=qx(t_now)+dt*v*cos(qfi(t_now+1));

qz(t_now+1)=qz(t_now)+dt*v*sin(qfi(t_now+1));

W=-0.000001*p1(t_now)*g/v*tan(qgamma(t_now))+p2(t_now)*qomega(t_now)+p3(t_now)*(Mw*omega(t_now)+Md*delta(t_now));

tt(t_now+1)=tt(t_now)+W;

end;

qwe=fix(100*tt(length(t)));

progn_fi=qfi

progn_gamma=qgamma

progn_delta=qdelta

progn_u=qu

progn_omega=qomega

t=[t0:dt:tf+dt];

figure

plot(t, progn_fi);

figure

plot(t,progn_gamma);

figure

plot(t,progn_omega);

figure

plot(t, progn_delta);

figure

plot(t,progn_u);

%%

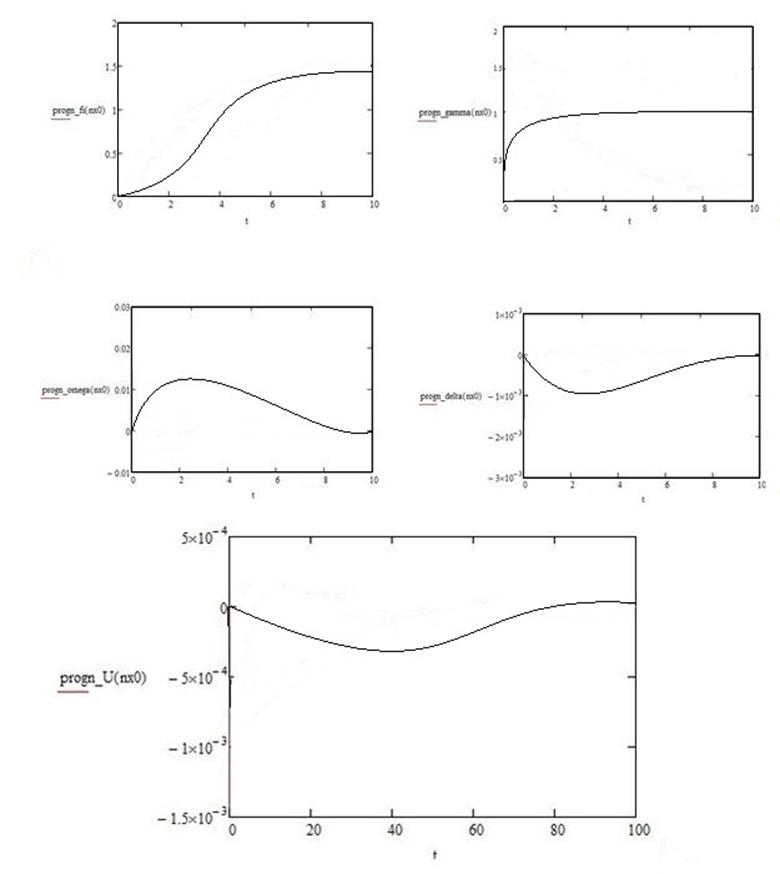
Приложение Б - Графики изменения исследуемых величин

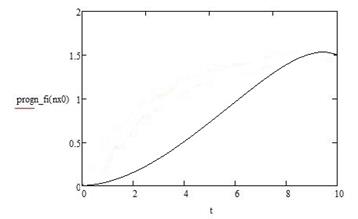
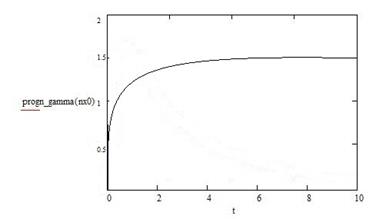
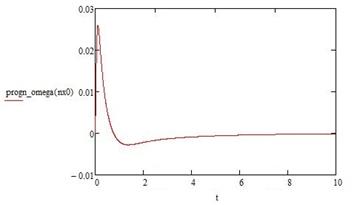
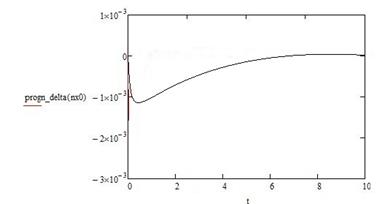
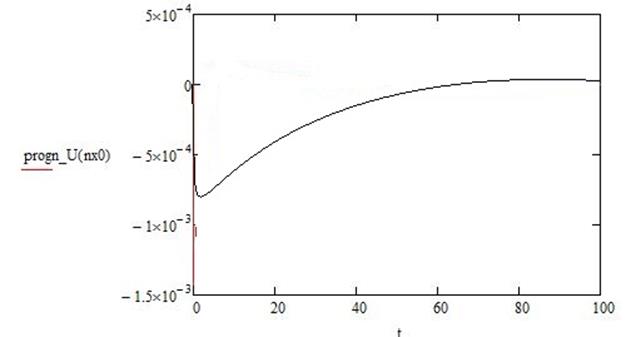
Приложение Б - Графики изменения исследуемых величин