Алгоритм оптимального разворота ЛА на заданный угол крена, страница 2

- внешние силы, действующие на самолет ;

- сила тяги двигателя ;

- внутренние кориолисовые силы инерции из-за движения масс внутри твердой      оболочки .

Тогда уравнения примут вид:

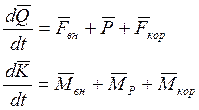                                              (3)

Причем, первое уравнение описывает движение центра масс относительно  БПЛА, а второе – движение  БПЛА относительно центра масс  БПЛА.

Наиболее удобно исследовать движение  БПЛА, пользуясь подвижными системами координат в начале с центром масс  БПЛА. При проектировании производной по времени от какого-либо вектора на оси любой подвижной системы координат Οxyz, вращающейся с угловой скоростью  относительно выбранной системы отсчета (неподвижной), должны быть применены известные из векторного анализа формулы:

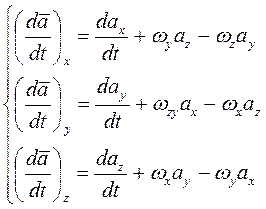                                                                          (4)

Движение центра масс  БПЛА

Пренебрегая скоростью и ускорением перемещения центра масс  БПЛА относительно его корпуса, производная от количества движения по времени будет равна:

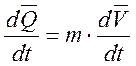                                                        (5)

Учитывая (4), разделяем полученные уравнения на проекции по осям XYZ, получим систему динамических уравнений движения в проекциях на оси системы координат, помещенных в центр масс  БПЛА:

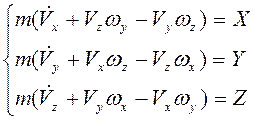                                                                            (6)

где X,Y и Z – проекции сил на соответствующие оси

Векторное уравнение движения центра масс с учетом того, что:

-   

-   - главный вектор аэродинамических  сил, приложенный в центре масс  БПЛА

-   - сила тяжести примет вид:

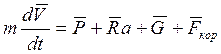                                                                            (7)

Наиболее простую и удобную форму система динамических уравнений движения центра масс  БПЛА примет, если векторное уравнение спроектировать на оси траекторной системы координат ox_кy_кz_к.

Применяя формулу (6) для проектирования левой части уравнения (7) и учитывая, что , получим:

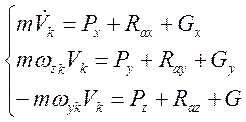                                                                             (8)

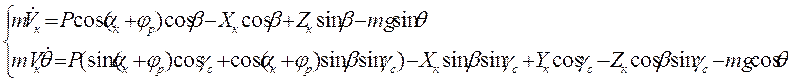                                                                                                                      (9)

Допущения:

-  рассматриваем продольное движение  БПЛА () тогда:

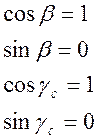
-  считаем самолет жестким телом, не учитываем кориолисовые силы инерции ;

-  не учитываем слагаемые, связанные с вращением Земли;

-  не учитываем изменение массу  БПЛА из-за выгорания топлива.

Тогда уравнения движения центра масс в траекторной системе примут вид:

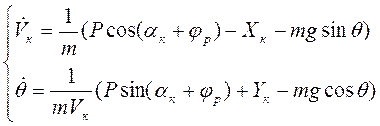                                   (10)

Движение относительно центра масс  БПЛА.

Динамические уравнения движения  БПЛА относительно его центра масс в проекциях на какие-либо оси могут быть выведены из уравнения момента количества движения системы переменного состава. Наиболее простую форму уравнения примут, если использовать для записи уравнений в проекциях главные центральные оси инерции  БПЛА. Направление этих осей относительно твердой оболочки  БПЛА совпадают со связанными осями координат. Учитывая (4), вычисляем проекции производной по времени от вектора кинетического момента (2)  БПЛА, получим систему скалярных уравнений:

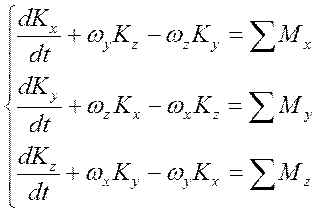                                                                 (11)

где

K_x, K_y, K_z - проекции вектора кинетического момента  БПЛА на связанные оси координат;

,,- проекции вектора абсолютной угловой скорости  БПЛА на те же оси;

-проекции главного момента аэродинамических сил и сил тяги относительно центра масс на те же оси.

Проекции вектора кинетического момента

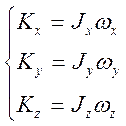                                                                                                 (12)

Тогда система уравнений (11) примет вид (без учета угловой скорости суточного вращения Земли, угловой скорости  БПЛА относительно нормальной системы координат и угловой скорости, возникающей из-за кривизны поверхности):

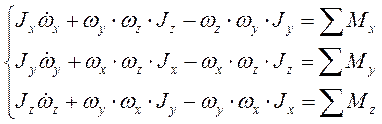                                                      (13)

Преобразовав систему (11) получим:

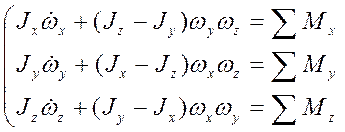                                                             (14)

               Допущения: