Алгоритм оптимального разворота ЛА на заданный угол крена, страница 5

Однако при достаточной сложности модели объекта управления это оказывается слишком трудоёмким, и приходится применять численные методы оптимизации.

Остановимся подробнее на важнейшем в теории оптимального управления понятии функционала.

Функционал – это числовая функция, определенная на некотором множестве функций. Другими словами, функционал формализует закон, по которому каждой функции X из некоторого множества, или класса, функций ставится в соответствие число J (рисунок 112):

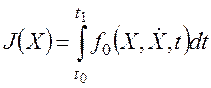.                                       (19)

Здесь X – возможно векторная функция, называемая также кривой или точкой функционального пространства, f₀ – интегрант.

Решение задачи оптимизации функционала состоит в нахождении его экстремума, а также функции  из заданного множества (допустимой области C функционального пространства), доставляющей этот экстремум:  или .

Понятие экстремума функционала, а также необходимые и достаточные условия достижения экстремума во многом совпадают с аналогичными понятиями и условиями для функции.

Функционал достигает локального экстремума на кривой x₀(t), если разность J(x₀)–J(x) сохраняет знак в некоторой окрестности x₀, т.е. при , где  – области определения функционала.

Если  для всех , то x₀ доставляет функционалу абсолютный максимум, если  – абсолютный минимум.

Первое необходимое условие достижения локального экстремума: dJ=0, где dJ – первая вариация, или первый дифференциал функционала.

Второе необходимое условие:  для минимума или  для максимума. Выполнение этого условия проверяется на кривых, удовлетворяющих первому необходимому условию. Здесь d²J – вторая вариация, или второй дифференциал функционала.

Достаточное условие локального экстремума состоит в одновременном выполнении первого и второго необходимых условий при строгом неравенстве во втором.

Оптимизация по критерию Красовского:

Для процесса описываемого уравнением:

, оптимальным в смысле минимума функционала

, является управление(при  )

, где V- решение линейного уравнения в частных производных:

,

Здесь V - непрерывная функция, имеющая непрерывные производные по x,t. В выражении для  I слагаемое  соответствует "работе" управлений в оптимальной системе.

Как классический функционал, так и функционал обобщенной работы А.А. Красовского дает возможность учесть гладкие ограничения на управление. Вообще говоря, процесс задания параметров функционала является многоэкстремальной многомерной задачей, решаемой в сочетании с теорией экспертных систем. Следует также отметить, что минимизация функционала обобщенной работы  эквивалентна минимизации функционала Больца, при дополнительном изопараметрическом ограничении

.

Это интегральное равенство характеризует задание обобщенной работы управлений в оптимальной системе . Отсюда происходит название ФОР.

Теперь , используя данный критерий применительно к системе (17) , запишем минимизируемый функционал

,     (20)

из которого :

,      (21)

с учетом ограничений Q1 и Q2 , запишем гамильтониан:

.    (22)

Определим из условия  управление как .

Далее определяются функции невязки и граничные условия :

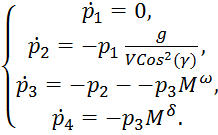      (23)

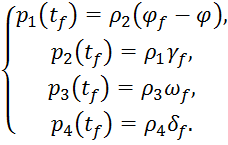     (24)

В случае учета ограничений на управление, система 23 примет вид:

     

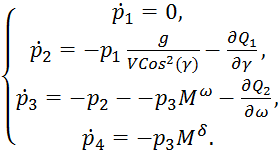
4. Алгоритм с прогнозирующей моделью

В данной задаче для решения поставленной задачи используется алгоритм с прогнозирующей моделью.

1) Находится гамильтониан:

.   (25)

2) находится управление из условия :

           (26)

3) Полагается :

,

4) Интервал оптимизации разбивается на шаги

5) Полагается t=t0

6) Система уравнений  17 интегрируется в прямом времени при u=0 от t до

7) Вычисляются граничные условия для p:

.

8) Интегрируются совместно системы 17 и 24 в обратном времени вдоль решения полученного в п.6

9) Вычисляется u0

10) С управлением, найденным в п.9 интегрируются система 17 на 1 шаг вперед.

11) Если  то алгоритм завершает работу. Если нет, то , возврат к п.6

Программный код, реализующий данный алгоритм представлен в приложении А.

5. Результаты моделирования