
















5. СПОСОБЫ СНИЖЕНИЯ ТРУДОЕМКОСТИ СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ
5.1. Основные методы уменьшения дисперсии оценки
Как видно из представленных в подразд. 3.3 соотношений, уменьшение дисперсии используемой при статистическом моделировании оценки искомой характеристики позволит пропорционально снизить количество опытов, необходимых для получения результата с заданной точностью.
Рассмотрим наиболее известные методы уменьшения дисперсии оценки на примере задачи определения математического ожидания некоторого показателя качества динамической системы со случайными параметрами.
Модель динамической системы задается в виде системы уравнений
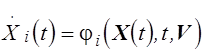 , i=1,2,...,n, (5.1)
, i=1,2,...,n, (5.1)
где ![]() - вектор переменных состояния системы;
- вектор переменных состояния системы; ![]() - вектор случайных параметров. Качество
системы характеризуется мгновенным значением переменной состояния
- вектор случайных параметров. Качество
системы характеризуется мгновенным значением переменной состояния ![]() в момент времени
в момент времени ![]() .
Таким образом, задача сводится к оценке математического ожидания
.
Таким образом, задача сводится к оценке математического ожидания ![]() = =
= =![]() .
.
При использовании
стандартной схемы статистического моделирования оценка ![]() для
заданной m-мерной ПРВ вектора
случайных параметров
для
заданной m-мерной ПРВ вектора
случайных параметров ![]() определяется по формуле (3.2), а
необходимое для обеспечения заданной точности количество опытов - по формуле
(3.19).
определяется по формуле (3.2), а
необходимое для обеспечения заданной точности количество опытов - по формуле
(3.19).
5.1.1. Метод выделения главной части
Решение системы (5.1)
![]() , которое, возможно, не может быть найдено
аналитически, заменяют приближенным выражением
, которое, возможно, не может быть найдено
аналитически, заменяют приближенным выражением ![]() ,
удобным для аналитических преобразований. Например:
,
удобным для аналитических преобразований. Например:
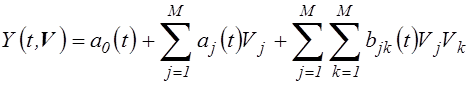
или для единственного случайного параметра
![]() , где
, где ![]() ,
, ![]() - некоторые функции времени.
- некоторые функции времени.
Вводится новая
переменная состояния ![]() и в системе уравнений (5.1)
выполняется замена переменной
и в системе уравнений (5.1)
выполняется замена переменной ![]() на Z путем подстановки:
на Z путем подстановки:
 ,
,
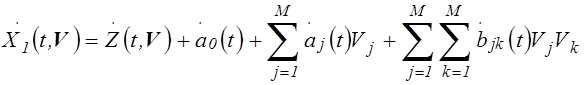
или
![]() ,
,
![]() .
.
Оценка искомого математического ожидания определяется в виде:
![]() , где первое слагаемое может быть найдено
аналитически:
, где первое слагаемое может быть найдено
аналитически:
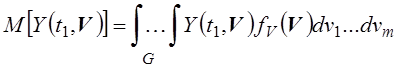 ,
,
G
-
область возможных значений вектора V, а второе слагаемое
определяется по методу статистического моделирования на основе многократного
решения полученной новой системы уравнений до момента времени ![]() :
: ![]()
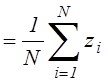 ,
, 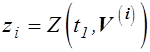 ,
, ![]() - i-я реализация вектора
случайных параметров, N - количество решений
системы уравнений для различных
- i-я реализация вектора
случайных параметров, N - количество решений
системы уравнений для различных ![]() .
.
При удачном выборе
функции ![]() дисперсия случайной величины
дисперсия случайной величины ![]() может оказаться существенно меньше, чем
дисперсия
может оказаться существенно меньше, чем
дисперсия ![]() , что и приведет к сокращению требуемого
количества опытов.
, что и приведет к сокращению требуемого
количества опытов.
Пример. Рассмотрим
достаточно простой пример, все необходимые расчеты для которого могут быть
выполнены точно на основе аналитических решений. Пусть требуется определить
математическое ожидание выходного сигнала X апериодического
звена 1-го порядка через 1 с после подачи на вход сигнала ![]() . Коэффициент передачи звена k=4. Постоянная времени и начальное значение выходного
сигнала - случайные:
. Коэффициент передачи звена k=4. Постоянная времени и начальное значение выходного
сигнала - случайные: 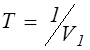 ,
, ![]() .
Параметр
.
Параметр ![]() распределен по равномерному закону в
интервале
распределен по равномерному закону в
интервале ![]() , параметр
, параметр ![]() - по равномерному
закону в интервале
- по равномерному
закону в интервале ![]() ,
, ![]() и
и ![]() статистически независимы. Допустимая
абсолютная погрешность результата
статистически независимы. Допустимая
абсолютная погрешность результата ![]() .
.
Искомое
математическое ожидание ![]() , дисперсия
, дисперсия ![]() и необходимое количество опытов могут быть
оценены на основе статистического моделировани или определены аналитически.
и необходимое количество опытов могут быть
оценены на основе статистического моделировани или определены аналитически.
Сначала получим точное решение задачи. Изменение сигнала X во времени описывается дифференциальным уравнением
![]() .
(5.2)
.
(5.2)
Решение (5.2) имеет
вид: ![]() .
.
Для t=1 с учетом статистической независимости
параметров ![]() и
и ![]() получим:
получим:
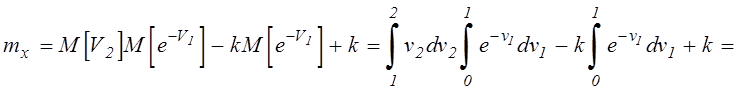
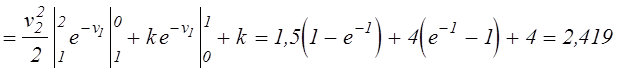 ,
,
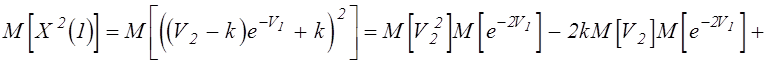
![]() ,
,
![]() .
.
С учетом известной ![]() по (3.19) оценим количество опытов,
необходимое для оценки
по (3.19) оценим количество опытов,
необходимое для оценки ![]() методом статистического
моделирования с погрешностью, не превышающей
методом статистического
моделирования с погрешностью, не превышающей ![]() (при
доверительной вероятности 0,997):
(при
доверительной вероятности 0,997):
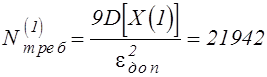 .
.
При решении этой же
задачи методом статистического моделирования на основе итерационного алгоритма
(с. 53) получены следующие оценки (БЭЙСИК, IBM PC, объем начальной серии опытов
![]() ):
):
![]() ,
, ![]() ,
, ![]() .
.
В процессе решения фактически
выполнено ![]() опытов.
опытов.
Применим теперь к этой задаче метод выделения главной части. Приближенное решение уравнения (5.2) выберем в виде
![]() . (5.3)
. (5.3)
Его математическое ожидание при t=1 легко вычисляется аналитически:
![]() .
.
Выполним в уравнении (5.2) замену переменной:
![]() ,
,
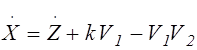 .
.
Получим новое
уравнение 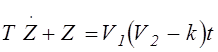 , аналитическое решение которого имеет вид:
, аналитическое решение которого имеет вид:
![]() .
.
Для t=1 интегрированием аналитического решения получим:
![]() ,
, ![]() ,
, ![]() .
.
Таким образом,
представляется возможным для рассматриваемой задачи путем выделения главной
части в виде (5.3) сократить трудоемкость статистического моделирования в ![]() раза.
раза.
При контрольном статистическом моделировании на основе использованного выше алгоритма получены следующие оценки:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
В процессе решения
фактически выполнено ![]() опыта. На практике трудоемкость
моделирования сокращена в
опыта. На практике трудоемкость
моделирования сокращена в 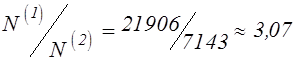 раза.
раза.
Выберем другой вариант приближенного решения уравнения (5.2)
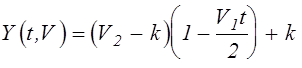 .
.
Для него получим:
![]() ,
,
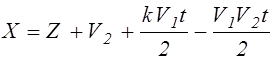 ,
,
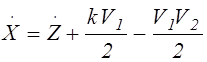 ,
,
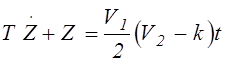 ,
,
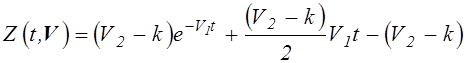 .
.
На основе
аналитического решения для t=1: ![]() ,
, ![]()
![]() ,
, ![]() - и
ожидаемый выигрыш в количестве опытов в
- и
ожидаемый выигрыш в количестве опытов в ![]() раз.
раз.
При контрольном
статистическом моделировании здесь были получены следующие оценки: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() , фактическое количество опытов
, фактическое количество опытов ![]() и выигрыш в трудоемкости в
и выигрыш в трудоемкости в ![]() раза.
раза.
5.1.2. Метод существенной выборки
Преобразуем общее
соотношение для определения математического ожидания ![]() =
=![]() по генеральной совокупности
следующим образом:
по генеральной совокупности
следующим образом:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.