1. Проведение серии объемом N опытов с натурной моделью с соблюдением основных требований статистического эксперимента (однородность условий и независимость отдельных опытов) и регистрацией реализаций случайных внешних воздействий на систему, имевших место в отдельных опытах.
В результате такого
эксперимента получают случайную выборку значений показателя качества системы ![]() , по которой на основе (5.13)
определяют оценку
, по которой на основе (5.13)
определяют оценку ![]() искомой характеристики, и случайную выборку измеренных
реализаций вектора внешних воздействий
искомой характеристики, и случайную выборку измеренных
реализаций вектора внешних воздействий ![]() , по которой определяют вектор оценок статистических
характеристик внешних воздействий
, по которой определяют вектор оценок статистических
характеристик внешних воздействий ![]() :
:
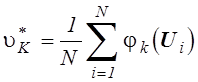 , k=1,2,...,K . (5.23)
, k=1,2,...,K . (5.23)
2. Построение
математической модели исследуемой системы, близкой к оригиналу в достаточной
степени, чтобы обеспечивалась чувствительность ее характеристик к
рассматриваемым внешним воздействиям. Проведение серии объемом N опытов с математической моделью с воспроизведением в
каждом опыте измеренных при натурном эксперименте реализаций вектора U и определение оценки ![]() статистической характеристики модели
по (5.14).
статистической характеристики модели
по (5.14).
3. Определение
расчетного значения статистической характеристики модели ![]() аналитическим методом или путем
статистического моделирования достаточно большого объема
аналитическим методом или путем
статистического моделирования достаточно большого объема ![]() . При определении
. При определении ![]() используется вектор оценок
используется вектор оценок ![]() , полученный по выборке ограниченного
объема N.
, полученный по выборке ограниченного
объема N.
Проанализируем характер результатов моделирования.
Оценка ![]() представляет собой случайную величину
с характеристиками:
представляет собой случайную величину
с характеристиками: ![]() ,
, 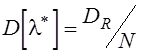 , где l
- точное значение искомой статистической характеристики, соответствующее
теоретически бесконечному количеству опытов,
, где l
- точное значение искомой статистической характеристики, соответствующее
теоретически бесконечному количеству опытов, ![]() - дисперсия показателя качества R.
- дисперсия показателя качества R.
Составляющие вектора ![]() представляют собой случайные
величины, которые при отсутствии систематических ошибок измерения внешних
воздействий имеют характеристики:
представляют собой случайные
величины, которые при отсутствии систематических ошибок измерения внешних
воздействий имеют характеристики: ![]() , где
, где ![]() - составляющие вектора истинных значений статистических
характеристик внешних воздействий,
- составляющие вектора истинных значений статистических
характеристик внешних воздействий, 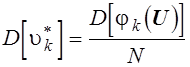 .
.
Оценка ![]() представляет собой случайную величину
с характеристиками:
представляет собой случайную величину
с характеристиками: ![]() ,
, 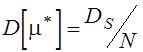 , где
, где ![]() - точное значение рассматриваемой статистической
характеристики математической модели, соответствующее теоретически бесконечному
количеству опытов с натурной и математической моделями,
- точное значение рассматриваемой статистической
характеристики математической модели, соответствующее теоретически бесконечному
количеству опытов с натурной и математической моделями, ![]() - дисперсия случайной величины S.
- дисперсия случайной величины S.
Расчетное значение ![]() в силу случайности
в силу случайности ![]() также является случайной величиной,
для получения характеристик которой при допущении о малой величине
также является случайной величиной,
для получения характеристик которой при допущении о малой величине ![]() (k=1,2,...K)
можно
использовать разложение в ряд Тейлора в окрестности точки
(k=1,2,...K)
можно
использовать разложение в ряд Тейлора в окрестности точки ![]() с учетом только первых степеней:
с учетом только первых степеней:
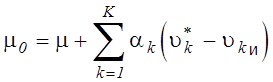 ,
, 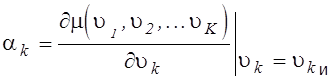 .
.
Тогда с учетом (5.23) получим
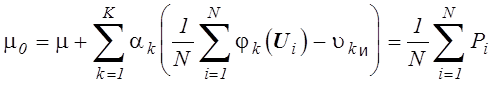 , где
, где
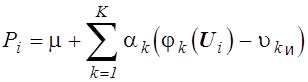 .
.
В результате ![]() ,
, 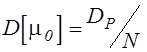 .
.
Аналогично можно получить корреляционные моменты связи:
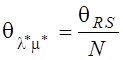 ,
, 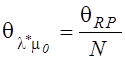 ,
, 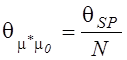 .
.
Оптимальная комбинированная оценка
характеристики l строится в линейной
форме: ![]() .
.
C учетом полученных
выше математических ожиданий из условия несмещенности ![]() .
.
Коэффициент c определяется из условия минимума дисперсии ![]() c учетом полученных соотношений для
дисперсий и корреляционных моментов связи:
c учетом полученных соотношений для
дисперсий и корреляционных моментов связи:
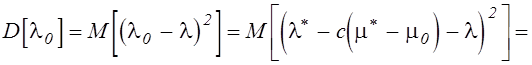
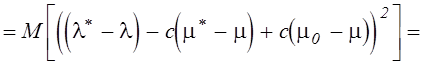
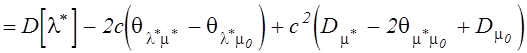 ,
,
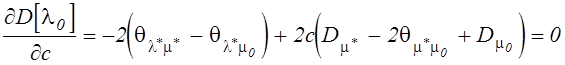 ,
,
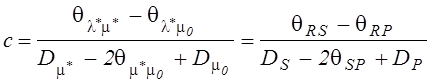 .
.
Удобно ввести в
рассмотрение новую случайную величину Q=S-P, для которой ![]() . Тогда с учетом теоретических соотношений
для определения дисперсии и корреляционного момента связей
. Тогда с учетом теоретических соотношений
для определения дисперсии и корреляционного момента связей
![]() ,
,
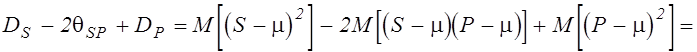
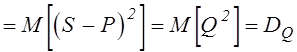 .
.
В результате 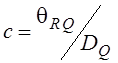 , и соотношение для оптимальной оценки
примет вид, аналогичный (5.16):
, и соотношение для оптимальной оценки
примет вид, аналогичный (5.16): 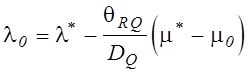 .
.
На практике возможно лишь использование оценки вида
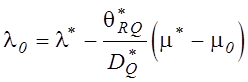 , где
, где ![]() ,
, ![]() - оценки корреляционного момента связи и дисперсии,
получаемые по N опытам,
- оценки корреляционного момента связи и дисперсии,
получаемые по N опытам,
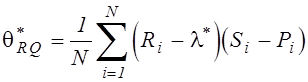 ,
, 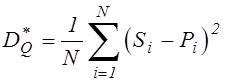 ,
,
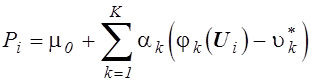 .
.
Коэффициенты ![]() определяются приближенно на основе
математической модели с использованием оценок составляющих вектора u:
определяются приближенно на основе
математической модели с использованием оценок составляющих вектора u:
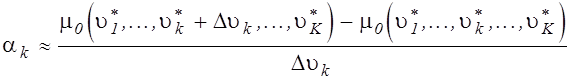 , k=1,2,...,K.
, k=1,2,...,K.
При оценке
эффективности метода по соотношению дисперсий оценок ![]() и
и ![]() получим:
получим: 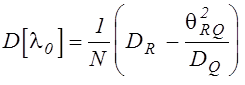 и возможный выигрыш в количестве опытов
и возможный выигрыш в количестве опытов 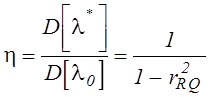 , где
, где 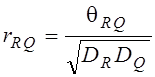 - коэффициент
корреляции случайных величин R и Q.
- коэффициент
корреляции случайных величин R и Q.
Остальные свойства
данного комбинированного метода также аналогичны рассмотренному выше. Однако
практически здесь трудно получить такой же значительный эффект, поскольку на
величину коэффициента ![]() влияют как упрощенность математической
модели, так и неидеальность измерительной системы, используемой при натурном
эксперименте.
влияют как упрощенность математической
модели, так и неидеальность измерительной системы, используемой при натурном
эксперименте.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.