Способы снижения трудоемкости статистического моделирования, страница 5

Соотношения (5.17) и (5.20) и в этом случае сохраняются, но квадрат коэффициента  здесь определяется следующим образом:

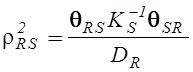                                ,                                                      (5.22)

где  - матрица-столбец.

На практике вместо (5.21) приходится использовать оценки вида

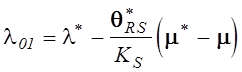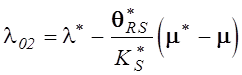, , достаточно близкие к ней по точности при . Здесь  - матрица-строка,  - квадратная матрица оценок корреляционных моментов связи,

, ,

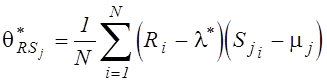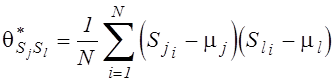j=1,2,...,m;  l=1,2,...,m.

С учетом полученных основных соотношений метода ясно, что здесь не предусматриваются какие-либо ограничения на форму упрощенной модели даже с точки зрения используемой в качестве ее основы математической схемы. Важна лишь степень корреляционной связи реакций основной и упрощенной моделей. Поэтому в качестве упрощенной модели обычно используют одну или несколько моделей простейших динамических систем, звеньев, нелинейных элементов и т. п. С увеличением m выигрыш от использования комбинированного метода возрастает [30].

Пример 1.  Вернемся к примеру, рассмотренному в подразд. 5.1. Выберем упрощенную модель в форме безынерционного нелинейного звена с двумя входами  и  и уравнением . Для упрощенной модели будем определять математическое ожидание выходного сигнала Y. Тогда, используя принятые выше обозначения, получим , S=Y. Определим на основе аналитических решений все численные характеристики задачи:

;   ;   ;

;

;

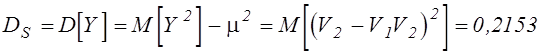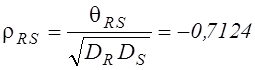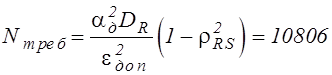;  , ожидаемый выигрыш в количестве опытов по сравнению со стандартной схемой статистического моделирования в  раза.

При контрольном статистическом моделировании с использованием соответствующей модификации итерационного алгоритма получена оценка  при фактическом количестве опытов N=12089, фактический выигрыш в количестве опытов - примерно в 1,8 раза.

Построим теперь упрощенную модель в виде совокупности двух нелинейных элементов с уравнениями  и 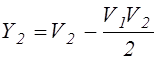. Будем для нее рассматривать векторы ,  . В соответствии с (5.21), (5.22) для m=2 и с учетом  основные расчетные соотношения будут иметь вид:

,

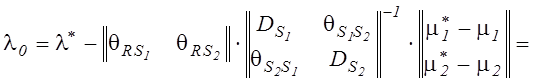
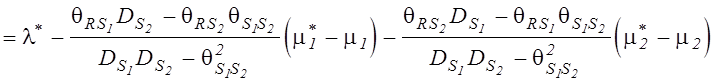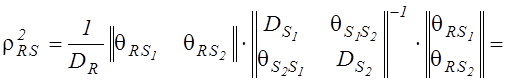
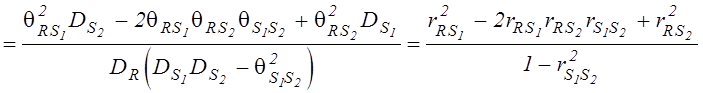, где , ,  - коэффициенты корреляции соответствующих пар случайных величин.

Получим все необходимые численные характеристики на основе аналитических решений:  ;  ;  ;  ;  ;

;   ;   ; 

;   ;

;   ;

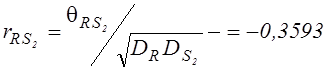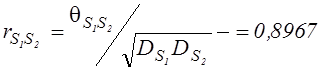;    и ожидаемый выигрыш в  раза.

При контрольном статистическом моделировании получена  при фактическом количестве опытов N=2150 и выигрыше в трудоемкости в 10,2 раза по сравнению со стандартной схемой моделирования.

Пример 2. Применим построенную в предыдущем примере упрощенную модель с m=2 для определения других статистических характеристик основной модели:  и .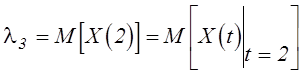

Точное значение , следовательно, , и необходимое для обеспечения требований задачи по точности количество опытов при статистическом моделировании по стандартной схеме  -  22500.  При контрольном моделировании потребовалось  22497  опытов. Результат: .

При оценке  комбинированным методом случайная величина R является дискретной:

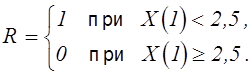
Получить точные значения всех численных характеристик задачи аналитическим методом здесь затруднительно. Поэтому ограничимся данными статистического моделирования на основе итерационного алгоритма: ;  ;  ;  ;   при фактическом количестве опытов 6780 и выигрыше в трудоемкости в 3,3 раза.

Для  точные значения: ,  и для стандартной схемы статистического моделирования . При контрольном моделировании потребовалось 34762 опыта. Результат: .

При моделировании с использованием комбинированного метода получены следующие оценки: ; ; ;  ;   при фактическом количестве опытов 5392 и выигрыше в трудоемкости в 6,4 раза.

При  рассмотренный метод не может дать отрицательного эффекта [30]. Его эффективность повышается с увеличением m.

5.2.2. Оценка статистической характеристики  системы на основе

 совместного использования результатов натурного эксперимента

 и математического моделирования

Точность определения статистических характеристик системы на основе натурного эксперимента, ограниченная его малыми возможными объемами, может быть существенно повышена за счет совместной обработки результатов натурного эксперимента и математического моделирования. Предназначенный для решения этой задачи комбинированный метод предусматривает: