Способы снижения трудоемкости статистического моделирования, страница 4

Рассматриваемый здесь метод предусматривает проведение статистических экспериментов объема N для основной и упрощенной моделей , а также определение рассматриваемых статистических характеристик упрощенной модели аналитически.

Определяемый по основной модели показатель качества исследуемой системы R в общем случае представляет собой некоторую функцию от значений ее переменных состояния: . В качестве статистической характеристики основной модели будем рассматривать . В результате проведения серии опытов получим выборку значений показателя качества  и определим оценку l стандартным способом:

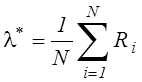                                             .                                                            (5.13)

Для упрощенной системы  в общем случае  рассматривается  m-мерный вектор статистических характеристик  и его оценка

                                                  ,                                                             (5.14)

где компоненты вектора S также являются некоторыми функциями переменных состояния упрощенной модели.

Уточненная оценка l строится в линейной форме:

, где B и C - некоторые m-мерные векторы-строки.

Рассмотрим подробно простейший случай, соответствующий m=1:

.                                                    (5.15)

Коэффициенты для (5.15) определяются в соответствии с условиями несмещенности и эффективности (минимума дисперсии) оценки.

Условие несмещенности имеет вид

 или .

С учетом (5.13), (5.14) получим: , . Кроме того, очевидно: . В результате , и поскольку в качестве l и m могут рассматриваться различные статистические характеристики, окончательно имеем:

b+c=0,  a=1, .

Найдем дисперсию :

.

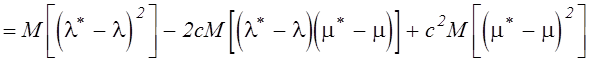Поскольку l и m - константы, а  и  определяются по (5.13), (5.14) через суммы независимых случайных величин, имеем:

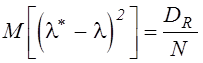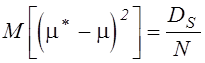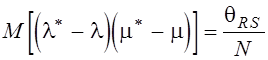,  ,  , где ,   - дисперсии, - корреляционный момент связи случайных величин R и S. В результате .

Применив к  первое необходимое условие экстремума по аргументу c, получим:

, 

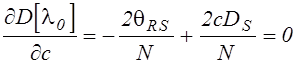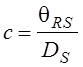
и окончательно:

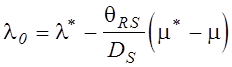                                         .                                            (5.16)

Смысл соотношения (5.16) состоит в пересчете значения ошибки оценки , которую удается найти точно, в поправку для уточнения оценки искомой характеристики l.

Для оценки эффективности метода определим дисперсию оценки (5.16):

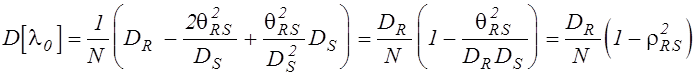, где  в рассматриваемом одномерном случае совпадает с коэффициентом корреляции случайных величин R и S  ,  [20].

Дисперсия определяемой стандартным методом оценки (5.13), как известно, равна .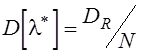

Отношение этих дисперсий дает выигрыш в количестве опытов с основной моделью, обеспечиваемый рассматриваемым методом:

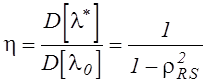                                         .                                               (5.17)

Очевидно, с увеличением  эффективность метода повышается.

С учетом исходной постановки задачи ясно, что точное значение  определить невозможно. Кроме того, вид упрощенной модели может оказаться таким, что не будет обеспечено и точное определение  аналитическим способом. Поэтому вместо (5.16) на практике используются оценки вида

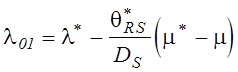,                                             (5.18)

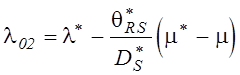,                                            (5.19)

где оценки корреляционного момента связи  и дисперсии  определяются по результатам тех же N опытов, что и , :

,  .

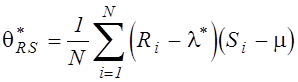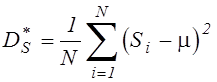При  различие в точности оценок ,  и  незначительно [30].

Требуемое для получения результата с погрешностью не выше  количество опытов можно оценить в процессе моделирования в соответствии с (3.19):

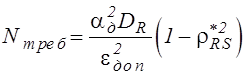                            ,                                                (5.20)

где 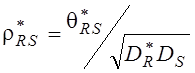 или ,  .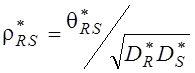

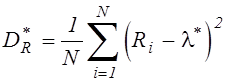Отметим, что при наличии ограничения на количество опытов с основной моделью использование рассматриваемого метода в силу (3.18) позволяет снизить погрешность оценки в  раз.

Если для упрощенной модели определяется m-мерный вектор статистических характеристик , оптимальная оценка для l имеет вид, аналогичный (5.16):

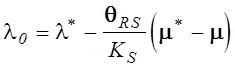                                ,                                                (5.21)

где  - матрица-строка корреляционных моментов связи случайной величины R и случайных величин  (j=1,2,...,m), ;  - матрица моментов вида (3.41) для случайного вектора S.