Способы снижения трудоемкости статистического моделирования, страница 2

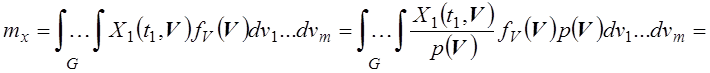
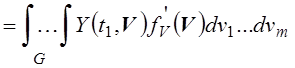                    .                                     (5.4)

Из соотношения (5.4) следует,  что искомое математическое ожидание  совпадает с математическим ожиданием новой функции 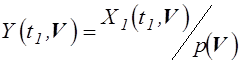, для которой вектор случайных параметров V имеет плотность распределения вероятностей . Это математическое ожидание может быть определено на основе статистического моделирования:

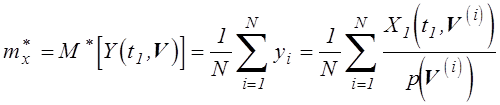                       .                    (5.5)

Причем при удачном выборе функции  дисперсия оценки (5.5) может оказаться существенно ниже, чем дисперсия оценки  по (3.2).

Функция p может иметь в качестве аргументов только часть случайных параметров задачи. В любом случае она должна удовлетворять условию:

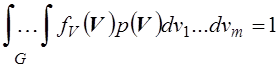                                     .                                          (5.6)

Для достижения наибольшего эффекта функцию  следует выбирать приблизительно пропорциональной  [17].

Пример. Выберем для рассмотренного выше примера функцию p в виде

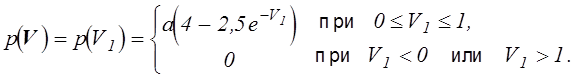                                  (5.7)

Из условия (5.6) найдем коэффициент a:

,  .

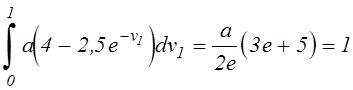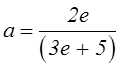Задача оценки  сводится к оценке математического ожидания новой случайной функции

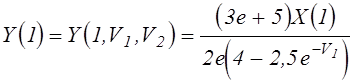, где  - решение уравнения (5.2) при t=1, параметр  должен иметь распределение (5.7), а параметр  - исходное распределение, равномерное в интервале .

Точное значение дисперсии функции  может быть найдено следующим образом:

,

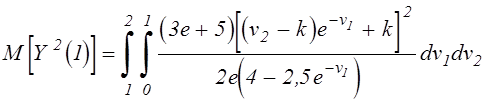                           .                  (5.8)

Значение интеграла (5.8) может быть получено только численным интегрированием и составляет . В результате , требуемое количество опытов для оценки  на основе статистического моделирования с заданной точностью  и ожидаемый выигрыш в трудоемкости - в  раза. Отметим, что закон распределения (5.7) не поддается воспроизведению по методу обратных функций. Следовательно, генератор для случайного параметра  придется строить, например, по методу Неймана, и в результате выигрыш в общей трудоемкости решения задачи окажется несколько ниже.

При контрольном статистическом моделировании с использованием генератора, построенного по методу Неймана, здесь были получены следующие оценки: , , , фактическое количество опытов  при 6194 обращениях к генератору случайных чисел и выигрыш в трудоемкости в 4,2 раза.

Для сравнения отметим, что при выборе

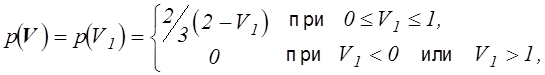
аналогичном успешно использованному выше выбору главной части, получим , и рассмотренный метод дает значительный отрицательный эффект.

5.1.3. Метод расслоенной выборки (выборка по группам)

В соответствии с данным методом область G возможных значений случайного вектора разбивается на K непересекающихся областей : . Метод предполагает проведение статистического моделирования для каждой из областей  с использованием для вектора случайных параметров плотностей распределения вероятностей

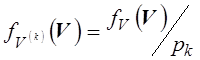                                                    ,                                            (5.9)

где  - вероятность попадания случайного вектора V в область :

.

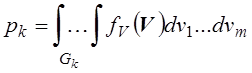Если для области  выполним  опытов, получим оценку математического ожидания искомого показателя для данной области:

.

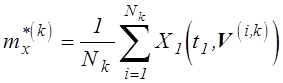Результирующая  оценка    должна рассматриваться как дискретная случайная величина, значения которой  наблюдаются с вероятностями . Тогда результирующая оценка определяется усреднением:

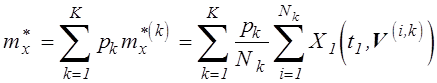                             .                         (5.10)

Общее количество опытов .

Соответствующие аналитические соотношения для генеральной совокупности с учетом (5.9) имеют вид

.

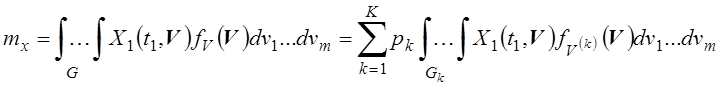Определим дисперсию оценки (5.10), имея в виду, что все  слагаемые - независимые случайные величины [10, 20]:

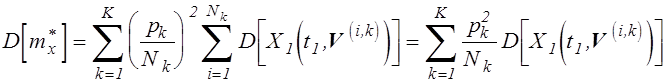 .  (5.11)

Дисперсия случайной величины 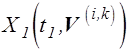 может быть оценена по результатам статистического моделирования или определена аналитически следующим образом:

,

,

.

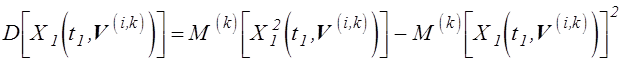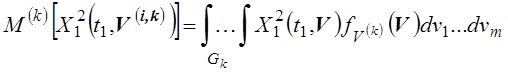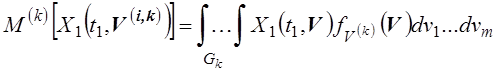Введя в рассмотрение доли от общего количества опытов, соответствующие областям , , 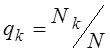на основе (5.11) и (3.19) получим соотношение для определения количества опытов, необходимого для получения результата с погрешностью не выше :

,

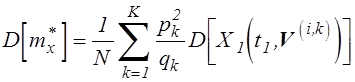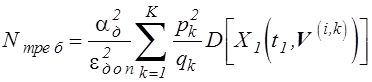                                         .                       (5.12)