Способы снижения трудоемкости статистического моделирования, страница 3

При удачном разбиении области G и удачном выборе соотношения количества опытов для отдельных областей  дисперсия оценки (5.10) может быть существенно снижена. Из теории [17] известно, что оптимальные по критерию минимума дисперсии (5.11) значения  должны быть пропорциональны произведениям 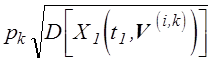. На практике значения дисперсий для отдельных областей, как правило, априорно неизвестны. Поэтому значения  выбираются на основе предварительного анализа задачи или непосредственно в процессе статистического моделирования на основе соответствующей модификации итерационного алгоритма определения необходимого количества опытов.

Пример. Разобьем для рассмотренного выше примера область возможных значений параметра  на две части: и . Тогда ,  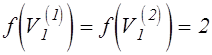в пределах соответственно  и . Выберем , .

На основе аналитических решений получим:

,  ,  ,

,  ,  ,

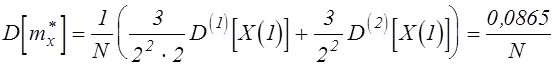, прогнозируемое в соответствии с (5.12) количество опытов, необходимое для обеспечения заданной точности,  и ожидаемый выигрыш в трудоемкости в 2,8 раза.

При статистическом моделировании для начальной серии опытов были приняты , которые уточнялись вместе с  на каждом цикле итерационного алгоритма с учетом получаемых оценок дисперсий. Получены следующие результаты: , , , , , , фактическое общее количество опытов  и достигнутый выигрыш в трудоемкости в 2,4 раза.

В заключение отметим, что в общем случае рассмотренные методы не дают гарантированного положительного эффекта. Как видно даже из рассмотренного простейшего примера, эффективность их применения определяется точностью прогнозирования результатов решения задачи. В наибольшей степени это характерно для методов выделения главной части и существенной выборки. Поэтому для сложных моделей, где точное прогнозирование результатов затруднительно, наиболее удобным оказывается метод выборки по группам.

5.2. Комбинированные методы получения оценок

Группа методов, разработанных В. Н. Пугачевым [30], преследует цель повысить точность (или соответственного снизить трудоемкость) статистического эксперимента со сложной математической, натурной или другой трудоемкой моделью системы за счет проведения параллельного исследования упрощенной модели и совместной обработки результатов.

Основные идеи этих методов состоят в следующем:

1. Упрощенная модель строится таким образом, чтобы обеспечивалась возможность аналитического исследования и статистического эксперимента со значительно меньшей трудоемкостью по сравнению с основной моделью.

2. Должна быть обеспечена определенная аналогия упрощенной и основной моделей, степень которой оценивается по корреляционной связи их реакций на одинаковые воздействия.

3. С основной и упрощенной моделями проводится параллельный статистический эксперимент одинакового объема при одинаковых воздействиях и оцениваются их статистические характеристики. Количество и виды статистических характеристик упрощенной системы, вообще говоря, могут не соответствовать статистическим характеристикам, определяемым для основной системы.

4. Для упрощенной модели определяются также точные значения рассматриваемых статистических характеристик и отклонения полученных оценок от точных значений.

5. Фактические значения погрешностей оценок статистических характеристик упрощенной модели используются для уточнения оценок статистических характеристик основной модели. Если обеспечивается достаточная степень корреляционной связи реакций основной и упрощенной моделей на одинаковые воздействия, то таким образом удается существенно уточнить результаты исследования основной модели.

5.2.1. Оценка  статистической  характеристики  сложной  математической

 модели  с  использованием  результатов  аналитического

  упрощенного  исследования

Уточним характер условий статистического эксперимента с основной и упрощенной моделями. Термином “воздействия” здесь обозначаются реализации случайных входных сигналов или значения случайных параметров модели, генерируемые для конкретного опыта с моделью. Серии опытов с основной и упрощенной моделями проводятся с обеспечением стандартных требований к статистическому эксперименту - однородность условий в смысле постоянства законов распределения воздействий и независимость результатов отдельных опытов. Но при этом отдельные параллельные опыты с основной и упрощенной моделями проводятся для идентичных реализаций случайных воздействий.