Исследование линейных электрических цепей. Анализ динамических свойств исследуемой электрической цепи с точки зрения быстроты затухания переходного процесса, формы кривой, склонности цепи к колебаниям

Балтийский государственный технический университет

«Военмех» им. Д.Ф. Устинова

Кафедра И3

«Информационные системы и компьютерные технологии»

Домашнее задание №1

По дисциплине: «Основы теории управления»

Тема: «Исследование линейных электрических цепей»

Выполнил:

Студент Тихонов А.Ю.

Группа И383

Преподаватель:

Доц. Емельянов В.Ю.

Санкт-Петербург

2010

Задание

Рассчитать переходный процесс в линейной электрической цепи и исследовать ее динамические свойства.

1.   Построить переходную характеристику U_вых(t) при нулевых начальных условиях и при U_вх(t)=a·1(t) (a=1).

2.   Построить частотные характеристики: амплитудно-фазовую частотную характеристику W(jω) (построение выполняется на комплексной плоскости), амплитудную частотную характеристику [A(ω)], фазовую частотную характеристику [φ(ω)], логарифмическую амплитудно-частотную характеристику (ЛАХ) L(ω) и логарифмическую фазовую частотную характеристику (ЛФЧХ) φ(ω).

3.   Проанализировать динамические свойства исследуемой электрической цепи с точки зрения быстроты затухания переходного процесса t_П, формы кривой, склонности цепи к колебаниям (оценить период колебания T_П, собственную частоту колебаний ω₀, частоту среза ω_С, параметр затухания ξ), оценить как преобразует исследуемая цепь входной сигнал и какой вносит фазовый сдвиг.

Вариант 1-4:

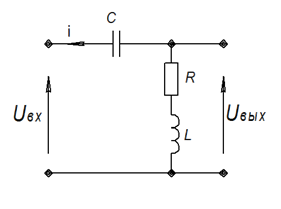
Данные к схеме:

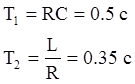
1.1.   Составим уравнения для описания исследуемой линейной электрической цепи и запишем их в дифференциальной форме:

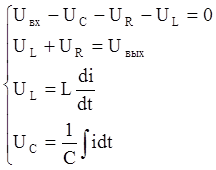
Преобразуем исходные уравнения для приведения к дифференциальной форме:

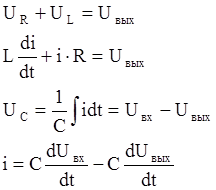
Тогда дифференциальное уравнение будет иметь вид:

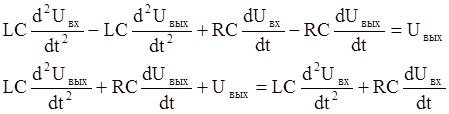
1.2    Запишем исходное дифференциальное уравнение в операторной форме:

1.3    Преобразуем операторное уравнение к виду, удобному для перехода от изображений к оригиналам:

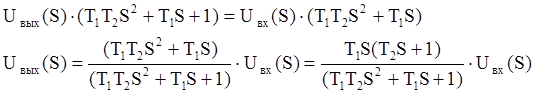
1.4    Получим переходную характеристику как оригинал отображения выходного сигнала при нулевых начальных условиях и при действии входного сигнала следующего вида:

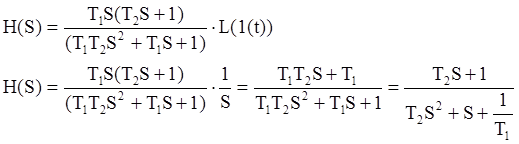
Получим оригинал функции H(S) с помощью формулы разложения для случая пары комплексно-сопряженных корней из таблиц обратного преобразования Лапласа:

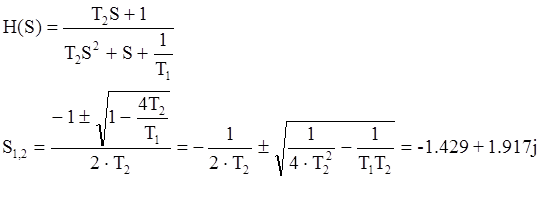
Тогда используя теорему разложения получим следующее выражения для переходной характеристики:

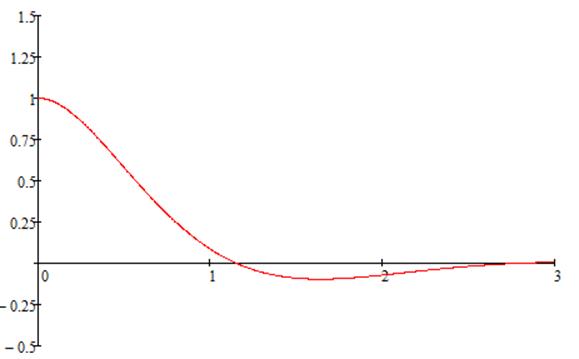
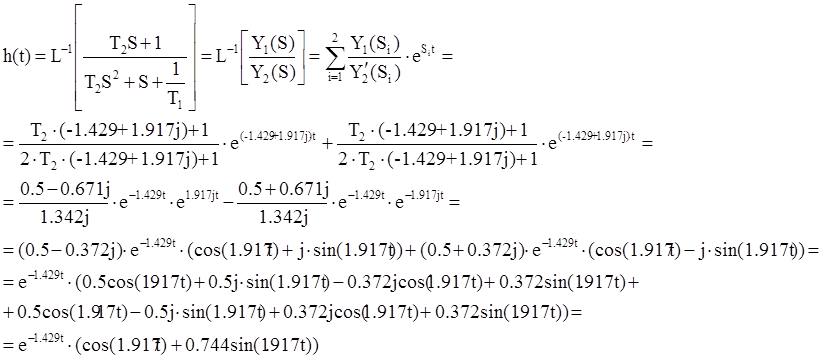 График полученной переходной характеристики будет выглядеть следующим образом:

2.1    При определении частотных характеристик будем полагать, что на вход линейной цепи подается гармоническое воздействие вида:

Так как цепь линейная, то

Передаточная функция звена определяется следующим образом:

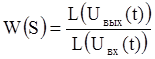
Изображения по Лапласу входного и выходного сигналов определим из таблиц преобразований:

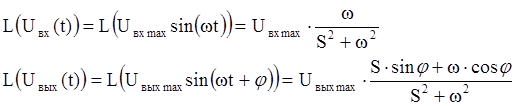
Тогда передаточная функция звена примет вид:

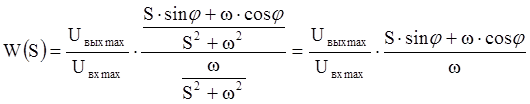
Комплексный коэффициент передачи определяется следующим образом:

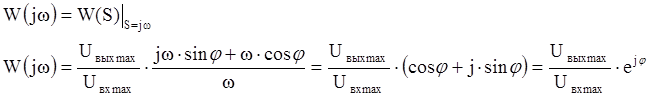
С другой стороны, передаточную функцию звена можно выразить из основного дифференциального уравнения цепи, записанного в операторной форме:

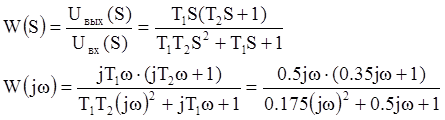
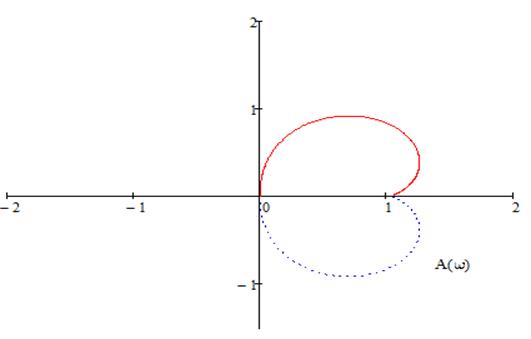
График полученной амплитудно-фазовой частотной характеристики  будет иметь вид: