Разработка линеаризованной математической модели возмущенного движения самолета

Московский Авиационный Институт

(Государственный Технический  Университет)

Кафедра 106

Отчет

о курсовой работе по дисциплине

«Теория оптимального управления»

Выполнил:

Преподаватель: Тюменцев Ю.В.

г. Москва,  2010 г.

Содержание

1.  Задание на курсовую работу.

2.  Исходные данные.

3.  Математическая модель возмущенного движения.

3.1. Уравнения поступательного движения центра масс самолета.

3.2. Уравнения вращательного движения самолета вокруг центра масс.

3.3. Линеаризация дифференциальных уравнений движения самолета.

4.  Вычисление матриц динамических коэффициентов.

4.1. Вычисление элементов матриц.

4.2. Выбор оптимизируемой величины.

5.  Синтез оптимального регулятора.

6.  Анализ характеристик рассматриваемой системы для разомкнутого и замкнутого случая.

7.  Исследование влияния вида оптимизирующего функционала на получаемое решение.

1.  Задание на курсовую работу

1.  Разработать линеаризованную математическую модель возмущенного движения самолета.

2.  Вычислить матрицы динамических коэффициентов и матрицы управления.

3.  Для линеаризованной модели продольного возмущенного движения самолета с постоянными скоростью и высотой полета решить задачу АКОР.

- решить квадратичное матричное уравнение Риккати;

- вычислить коэффициенты усиления оптимального регулятора;

- вычислить собственные значения замкнутой системы с оптимальным регулятором;

4.  Провести анализ характеристик рассматриваемой системы для   

разомкнутого и замкнутого случая.

- найти расположение полюсов для самолета без автопилота

(разомкнутая система) и с автопилотом (замкнутая система);

- определить частоты и относительные коэффициенты демпфирования  

для разомкнутой и замкнутой системы;

- построить логарифмические амплитудно-фазовые частотные характеристики для замкнутой системы для рассматриваемых регулируемых величин (угол отклонения стабилизатора);

- построить годограф Найквиста для замкнутой системы;

- определить реакцию замкнутой системы (каждой из переменных ее состояния) на ступенчатое воздействие по каждой из рассматриваемых регулируемых величин, найти характеристики переходного процесса

(время срабатывания, время переходного процесса, относительное перерегулирование).

5.  При выполнении синтеза закона управления и анализа характеристик получаемой в итоге системы провести исследование влияния вида оптимизирующего функционала на получаемое решение. А именно, проанализировать влияние значений компонент весовых матриц, т. е. изменения предпочтений по отдельным переменным состояния и  

управления. Для каждого из вариантов провести анализ по пунктам, перечисленным в 4, дать трактовку получаемых результатов, провести их сопоставление.

2.  Исходные данные

Самолет 8б – фронтовой истребитель.

 – площадь крыла самолета.

 - масса самолета.

  - производная момента тангажа самолета по углу отклонения стабилизатора.

 – средняя аэродинамическая хорда самолета.

 – высота полета самолета.

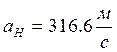 – скорость звука на заданной высоте.

 – угол скоса потока у горизонтального оперения.

 – атмосферное давление на заданной высоте.

– число М полета.

 – скоростной напор.

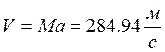 – скорость полета.

 – момент инерции самолета относительно оси Z.

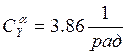 – производная коэффициента подъемной силы по углу атаки.

 – относительная координата фокуса самолета.

 – относительная координата центра тяжести самолета.

 – производная коэффициента момента самолета относительно оси Z по угловой скорости.

 – производная коэффициента момента самолета без горизонтального оперения относительно оси Z по угловой скорости.

3. Математическая модель возмущенного движения.

Вывод уравнений движения самолета.

Самолет рассматривается как абсолютно твердое тело. Уравнения пространственного движения свободного твердого тела в инерциальной системе координат имеют вид:

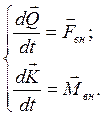
3.1 Уравнения поступательного движения центра масс самолета.

В неинерциальной системе координат(СК) добавляются переносная и кориолисова силы инерции:

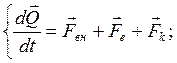
-переносная сила инерции;

-кориолисова сила инерции;

-сумма внешних сил;

;

Масса самолета считается постоянной: , тогда

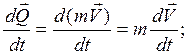
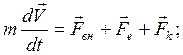
Это запись уравнения в неподвижной СК.

-локальная производная скорости в подвижной СК. Связь подвижной и неподвижной СК:

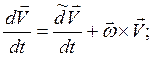
За неподвижную СК принята земная СК , начало которой находится в центре Земли, а оси жестко закреплены и вращаются вместе с ней.

;

;

;

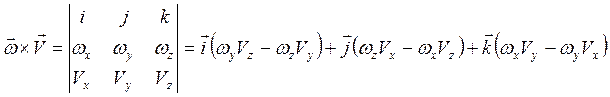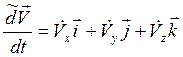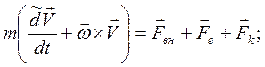
Это уравнение проектируется на оси подвижной СК:

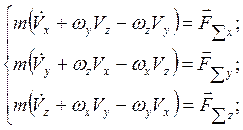
В качестве подвижной СК удобно взять траекторную, где:

 тогда получается:

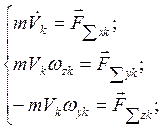(3.1)

Угловая скорость вращения траекторной СК относительно земной:

, где

- переносная угловая скорость нормальной СК относительно земной СК ; появляется вследствие кривизны Земли. До скорости 1000 м/с ее можно не учитывать.

- угловая скорость вращения траекторной СК относительно нормальной;

 проектируется на траекторную СК:

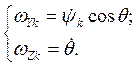(3.2)

Проекции сил, действующих на самолет, на траекторную СК:

Вес :

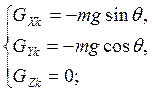(3.3)

Переносная сила инерции  учитывается в ускорении свободного падения.

Аэродинамическая сила  (3.4)

Сила тяги двигателя (при полете в вертикальной плоскости)

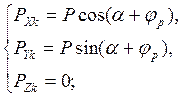
Кориолисова сила инерции практически не проявляется до скоростей порядка 1000 м/с, следовательно ее можно не учитывать.

Уравнения поступательного движения центра масс самолета получаем, подставив выражения для проекций сил и угловых скоростей (3.2)-(3.5) в систему уравнений (3.1):

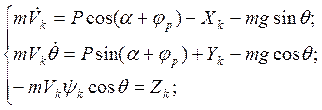(3.6)

К этой системе добавляются уравнения, связывающие пространственное