Определение вероятности безотказной работы системы в течение 500 часов

Балтийский Государственный Технический Университет

«Военмех» им. Д. Ф. Устинова

Кафедра И3

Домашнее задание по дисциплине

«Надежность»

Вариант 2.

Преподаватель:

Керножицкий В.А.

Студент:

Александров А.

Группа:

И391

Санкт-Петербург

2013

Задача 1.

Разрабатываемая система состоит из 1000 функционально необходимых элементов с постоянной интенсивностью отказов λ(t)=λ=10^-6 1/час. Определить вероятность безотказной работы системы в течение 500 часов, принять решение о необходимости повышения надежности, если требуемая величина  вероятности безотказной работы P_зад(800)≥0,90.

Решение:

Представим нашу систему из 1000 элементов в виде одного блока, тогда интенсивность отказов этого блока будет равна λ=10^-3 1/час. По формуле (1) оценим вероятность безотказной работы нашей системы.

P*(t)=e^-λ*t .                     (1)

P*(t)=0,607.

Для увеличения надежности системы можно применить резервирование системы. Зарезервируем всю систему:

 

Оценим вероятность безотказной работы после резервирования:

Q=(1-0,6)*(1-0,6)=0,16, P=1-Q=0,84.

Видим, что вероятность меньше заданной, поэтому используем раздельное резервирование отдельных частей системы для увеличения вероятности безотказной работы и уменьшения ее стоимости. Для этого разобьем систему на 20 последовательно соединенных подсистем, состоящих из 50 элементов(рисунок 1), и методом подбора выясним, сколько из них нужно зарезервировать.

Исходные данные для системы, состоящей из 50-ти элементов:

λ=5*10^-5 1/час

t=800 час

                                                                            

….

 

m=20

Рисунок 1.

Получим вероятность безотказной работы одного блока  без его резервирования:

Pm= e^-λ*t=0,961.

Вероятность безотказной работы каждого блока при его резервировании:

Pmr=1-(1-e^-λ*t)*(1-e^-λ*t)=0,998.

Вероятность безотказной работы всей системы при резервировании каждого блока составляет:

Ps=Pmr²⁰=0,97.

Видим, что полученная вероятность выше заданной, поэтому для уменьшения стоимости всей системы можно отказаться от резервирования одного или нескольких блоков. Методом подбора находим, что можно не резервировать 2 блока системы из 20-ти. При этом вероятность безотказной работы всей системы будет равна:

Ps=Pmr¹⁸*Pm²=0,898.

Полученная вероятность близка к заданной.

Задача 2.

Найти вероятность безотказной работы системы, имеющей заданную структурную схему надежности, если отказы разных устройств – события независимые, а вероятности исправной работы устройств составляют:

p₁(t)=0,90, p₂(t)=0,80, p₃(t)=0,80, p₄(t)=0,90, p₅(t)=0,70, p₆(t)=0,90, p₇(t)=0,80, p₈(t)=0,60, p₉(t)=0,96, p₁₀(t)=0,60, p₁₁(t)=0,60, p₁₂(t)=0,60, p₁₃(t)=0,60.

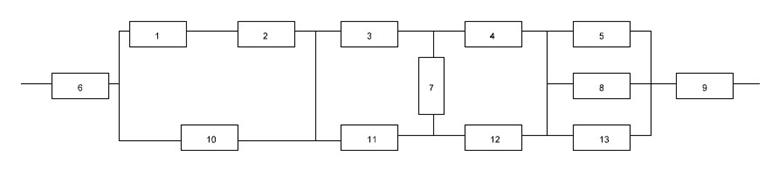
Для начала рассчитаем вероятность безотказной работы мостовой схемы:

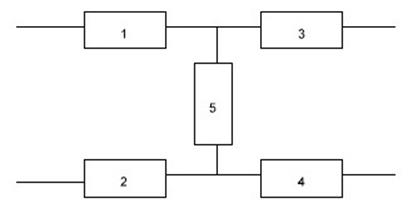
Вероятность безотказной работы мостовой схемы вычисляется по формуле:

P_моста = P₁P₃+ P₂P₄+ P₁P₄P₅+ P₂P₃ P₅ – P₁ P₃ P₄ P₅ – P₁ P₂ P₃ P₄ – P₁ P₂ P₄ P₅– P₁ P₂ P₃ P₅

+2 P₁ P₂ P₃ P₅– P₂ P₃ P₄ P₅.

Подставив значения,  получаем P_моста=0,913.

Далее «сворачиваем» все остальные структуры:

Р_1-2= P₁ P₂=0,72,

Р_1-2,10=1-Q_1-2Q₁₀=0,888,

P_5,8,13=1-Q₅Q₈Q₁₃=0,952,

P_оьщ= P₆ Р_1-2,10 P_моста P_5,8,13 P₉=0,667