Плюсы и минусы уроков математики молодых учителей

Н. Г. ВОРОБЬЕВА, В. Ф. ЕФИМОВ. Плюсы и минусы уроков математики молодых учителей// НАЧАЛЬНАЯ ШКОЛА, 2000. - №5- с.23-29.

Методисты районо и ИПКУ, администрация школ формируют свое мнение о профессио­нальной подготовленности, компетентности молодого учителя в основном по тому, как он проводит уроки, как эти уроки формируют и образовывают учащихся, в том числе и в обла­сти математики. В настоящее время молодым учителям предстоит отнюдь не простой, не очевидный выбор содержания, методов, средств обучения математике, в каких бы тех­нологических рамках, педагогических моде­лях он ни работал, каким бы авторским, аль­тернативным концепциям ни отдавал предпо­чтения. От того, как учитель через урок, серию уроков достигает решения многообразных пе­дагогических проблем, зависит, состоялся ли он как профессионально-значимая личность.

В силу специфики нашей работы нам неод­нократно приходилось (в последнее время в ос­новном в школах Московской области) наблю­дать плюсы и минусы уроков математики учи­телей, работающих по различным программам и учебникам. Заметно стремление молодых учителей искать и находить методические ре­шения по внедрению сравнительно новых педа­гогических идей. Во многих школах при подго­товке уроков ищущие, думающие учителя не ограничиваются материалом какого-то одного

учебника, тетради-учебника или учебного по­собия. Зачастую при работе с учебниками ново­го поколения (И. И. Аргинская, Н. Б. Истомина, Л. Г. Петерсон, Б. П. Гейдман, Г. Г. Микулина, В. Г. Тарасов и др.) у учащихся на партах нахо­дятся и традиционные, проверенные годами учебники математики (М. И. Моро, М. А. Бантова и др.) или обновленные учебники, в автор­ский коллектив которых вошли С. В. Степано­ва, С. И. Волкова. С одной стороны, это позво­ляет констатировать наличие комплексного ис­пользования основного средства обучения -учебников, в которых заложены новейшие педа­гогические, методические воззрения ученых, направленные на всестороннее развитие уча­щихся, на гуманизацию и гуманитаризацию об­разования, на формирование общей математи­ческой культуры. С другой - в комплексном ис­пользовании учебников существует опасность, которая на практике проявляется:

1)  в перегруженности уроков математики заданиями, отступлениями, на которые тратят­ся силы и время учащихся в ущерб усвоению с необходимой полнотой программных знаний, умений  и  навыков.  Перегруженность урока приводит  к  преждевременному  утомлению учащихся;

2) в неоправданном, а иногда и недопусти­мом переносе в новые условия опыта работы учителя по «накатанной» методике. Например, традиционное построение уроков без измене­ний переносится на уроки, когда учитель рабо­тает по программам и учебникам И. И. Аргинской, Л. Г. Петерсон, Н. Б. Истоминой и др., имеющих иную обучающую направленность.

Во многих уроках, посещенных нами, от­сутствуют или весьма нечетко, слишком обще формулируются цели урока. Общие цели обу­чения математике в течение 3 или 4 лет долж­ны постепенно конкретизироваться, находить свое отражение как в тематическом планирова­нии, разработках серий уроков, так и в каждом отдельном уроке, являющемся «кирпичиком» общего здания математического образования младшего школьника, обеспечивающего подго­товку к обучению в среднем звене школы. Нечеткое осознание целей урока не позволяет учителю достаточно ясно представить, обосно­ванно и квалифицированно выбрать из имею­щегося методического арсенала, а методистам увидеть и оценить, что дают используемые на уроке средства обучения, на формирование че­го направлены структурные, содержательные и процессуальные «единицы урока», под которы­ми понимаются этапы урока, упражнения, за­дания, познавательные акты, специально выст­роенные взаимодействия учителя и учащихся, учащихся друг с другом и т.п. Привнесенные в урок иногда в общем полезные, интересные «единицы» урока без учета целеполагания при­водят к распространенному и серьезному недо­чету - содержание урока, отдельные фрагмен­ты не соответствуют его целям.

Но даже правильное, безупречное опреде­ление целей бывает недостаточно для эффек­тивного их достижения. Анализируя уроки (конспекты уроков) молодых учителей, можно констатировать, что многие методические ошибки, просчеты являются следствием того, что учителя не владеют технологией разработ­ки урока, которая предполагает единство со­держания, методов и форм обучения. Основа технологии построения современного урока - постановка в соответствии с его целями учеб­ных задач. Исходя из концепции деятельностного подхода к обучению (развивающего обу­чения), предполагающей, что ученик - субъект обучения, необходимо учесть возрастные и ин­дивидуальные особенности учащихся, их вос­приятие учебного материала, возможности ре­шения поставленных учебных задач. Опреде­ляя содержательные единицы урока, необходи­мо определить, какие из поставленных учеб­ных задач, которые должны быть поняты и приняты учащимися, они решают. Урок для учащихся не должен быть только последова­тельностью заданий, которые они выполняют по предложению учителя. Часто урок остается времяпрепровождением или в лучшем случае «загадкой», которая мучает ученика, так как он не знает, зачем выполняет задания учителя; он просто привыкает к мысли, что так надо.

Важный момент урока - подведение его ито­гов. Часто итог урока не подводится либо заклю­чается в выставлении оценок, либо занятие завер­шается вопросом: «Чем занимались сегодня на уроке?» и получением ответа: «Решали примеры, задачи, считали устно» и т.п. Такое подведение итогов показывает, что учащиеся не поняли и не приняли учебных задач урока, не осознали свое продвижение в изучении учебного материала.

Другой часто встречающийся недостаток «открытых» уроков - их показательный харак­тер. Поэтому эти уроки, как правило, не носят обучающего характера, по типу это скорее уро­ки закрепления. На них выполняются упраж­нения на повторение пройденного, показыва­ются правильные ответы учащихся, а не орга­низация, например, поисков этих ответов.

Рассмотрим типичный, на наш взгляд, урок, проведенный в одной из школ Москов­ской области. Представим его конспект и по возможности прокомментируем его.

Тема: Письменное деление на числа, оканчивающиеся нулями (урок в III классе с объяснением нового).

Цели: I. Обучающие: 1) повторить прави­ла деления числа на произведение; 2) познако­мить с приемом деления на числа, оканчиваю­щиеся нулями; 3) совершенствовать умение решать задачи и навыки устного счета.

2.  Развивающие: развивать мышление, па­мять, внимание, математическую речь.

3.  Воспитывающие: формировать интерес к математике, воспитывать аккуратность при ведении записей в тетради.

План  урока:

I.  Организационный момент.

II.  Индивидуальная работа учащихся у дос­ки. Одновременно - упражнения в каллиграфии.

III.Закрепление изученного (индивидуальные задания - устные и письменные вычисления).

IV.Устные упражнения.

V.  Объяснение нового материала. Работа с учебником.

VI. Закрепление нового материала. Само­стоятельная работа.

VII. Домашнее задание.

VIII. Итог урока.

Ход  урока:

I.  Учитель сообщает тему урока, записан­ную на доске.

II. Двое учащихся вызываются к доске для са­мостоятельного выполнения следующих заданий:

1.  Дана шахматная доска. Надо определить ее площадь, если по длине расположено 8 ква­дратов, сторона каждого из которых - 2 см.

2.  Произвести действия: 10 км 075 м • 2 =…;  4 сут.3 ч • 5 =…; 8 т 415 кг : 3=

1.  Ширина прямоугольника в 4 раза короче, чем его длина, равная 36 см. Чему равен пери­метр прямоугольника?

2.  Произвести действия: 9 км 216 м • 2 =…; 5 сут. 7 ч • 3 =…; 5 км 265 м : 3 =

Пока двое работают у доски, учитель про­водит упражнения в каллиграфии; установка - писать красиво и аккуратно. Дети записывают под диктовку дроби: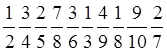

III. Закрепление изученного (индивидуальные задания на устные и письменные вычисления).