Система пульмофонографии легких. Акустические методы исследования легких. Сущность метода пульмофонографии, страница 8

Звуковое давление в конце главного бронха первого порядка и в начале долевых бронхов будет равно:

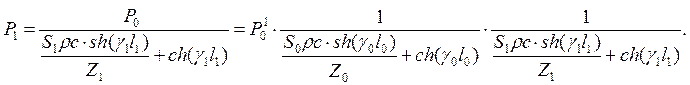 (8.2)

Соответственно, можно записать выражения для величины звукового давления в конце долевых, сегментарных и других бронхов высших порядков. Индексации параметров соответствуют рис. 8.5.

На основании формулы (8.2) можно записать выражение для звукового давления в конце бронха любого порядка трахеобронхиального дерева. В общем виде давление в конце некоторого концевого бронха, индекс которого m, равно:

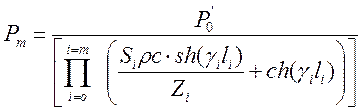.                                     (8.3)

Знаменатель представляет собой произведение величин (Sρc•sh(γl)•Z^-1 + ch(γl))^-1, характеризующих все бронхи, входящие в воздушный тракт, ведущий к рассматриваемому концевому бронху. Из формулы (8.3) видно важное свойство системы легочных звукопроводов - ее линейность, так как при изменении звукового давления на входе системы пропорционально изменяется звуковое давление во всех элементах системы. Следовательно, если в одном из бронхов вследствие причин местного характера произошло изменение звукового давления, пропорционально изменяется звуковое давление во всех звукопроводах, вентилируемых этим бронхом.

Представим геометрические параметры системы звукопроводов в явном виде и проанализируем формулу (8.3). Прежде всего, определим значения постоянных распространения γ_i и механических импедансов Zj.

Постоянная распространения γ = β + jαсодержит действительную часть β, представляющую собой коэффициент затухания, и мнимую часть jα (α - фазовая постоянная). Коэффициенты β и α в общем случае зависят от частоты звуковых колебаний и геометрических параметров звукопроводов, по которым распространяется звук, поэтому постоянной распространения, и ее составляющим, присваиваем индекс соответствующего звукопровода.

На практике, интервал частот акустических колебаний, на которых были попытки реализовать ПФГ исследования, лежит в пределах 50 - 200 Гц.

С учетом значения a и b [13] общее выражение звукового давления в участке паренхимы имеет вид:

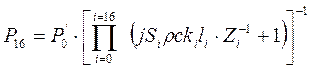.                                              (8.4)

Оценим значения механических импедансов Zi, сосредоточенных на концах бронхов, входящих в рассматриваемый воздушный тракт. В основу расчета импедансов Zi положен принцип, представленный на рис. 8.5.

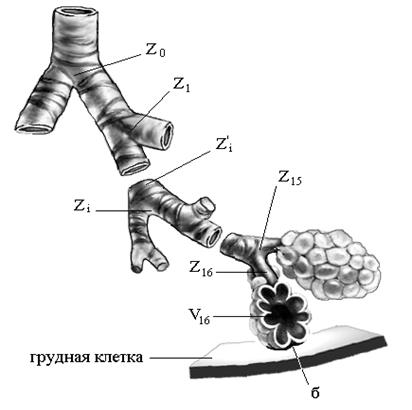
Рис. 8.5 – Схема распределения механических импедансов в бронхиальном дереве.

Механический импеданс, сосредоточенный на конце бронхиолы 16-го порядка, представляет собой совокупность параллельно присоединенных импедансов альвеол - резонаторов и приведенного импеданса грудной клетки. Затем определим импеданс в точке приложения силы, т е в начале бронхиолы 16 – го порядка. На следующем этапе определим импеданс в начале бронхиолы 15-го порядка, считая, что механический импеданс, сосредоточенный на конце этой бронхиолы равен сумме параллельно присоединенных импедансов резонаторов к концу бронхиолы.

Подставив выражение для импеданса в (8.4), выражение для звукового давления в участке паренхимы имеет вид:

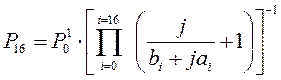.                                                   (8.5)

Давление, измеряемое акселерометром, установленным на участке грудной клетки равно модулю последнего выражения:

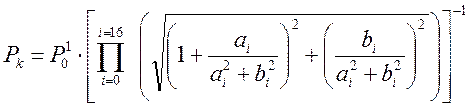.                 (8.6)

Таким образом, звуковое давление в участке паренхимы определяется произведением выражений в квадратных скобках, записанных для каждого бронха, входящего в ветвь воздушного тракта, ведущего к исследуемому участку паренхимы.

После упрощения уравнения (8.6) и приняв показатели среднестатистических размеров легких [14] была получена формула пригодная для практических расчетов в виде:

,                               (8.7)

В формуле (8.7) имеется единственный член V₁₆, меняющийся в процессе дыхания. Площадь соприкосновения участка паренхимы 16-го порядка с внутренней поверхностью грудной клетки s в процессе дыхания практически не изменяется.

Функция P_k = f(V₁₆), одновременно представляющая собой в общем, виде амплитудно-частотную характеристику воздушного тракта идеальной модели, позволяет оценивать акустические характеристики системы легочных звукопроводов и грудной клетки.