Лекция 14.Применение критерия устойчивости Найквиста с использованием логарифмических частотных характеристик. Определение запасов устойчивости
Критерий Найквиста обеспечивает анализ устойчивости также и на основе логарифмических частотных характеристик.
Для общего случая удобно использовать форму критерия, основанную на подсчете переходов. При этом следует учитывать, что переходам АФХ через горизонтальную ось левее точки (-1; 0j) на комплексной плоскости для логарифмических характеристик будут соответствовать переходы ЛФЧХ j(w) через горизонтальную ось на участках, где ЛАХ L(w)>0. Положительным является переход в направлении увеличения значений j(w), то есть сверху вниз, отрицательным – переход в обратном направлении.
Поскольку логарифмические частотные характеристики строятся для положительных частот, критерий сводится к соблюдению равенства:
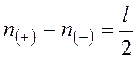 , где
n(+) –
количество «положительных» переходов, n(-) – количество «отрицательных» переходов, l - количество корней знаменателя передаточной функции
разомкнутой системы, лежащих в правой полуплоскости.
, где
n(+) –
количество «положительных» переходов, n(-) – количество «отрицательных» переходов, l - количество корней знаменателя передаточной функции
разомкнутой системы, лежащих в правой полуплоскости.
Для систем, нейтрально устойчивых в разомкнутом состоянии, дополняющие АФХ дуги принимают вид вертикальных прямых на соответствующих частотах:
- для нулевого корня от уровня j(w)=0 до 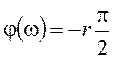 ;
;
- для мнимого корня вверх на p, то есть в пределах разрыва ЛФЧХ.
Вернемся к некоторым рассмотренным выше примерам.
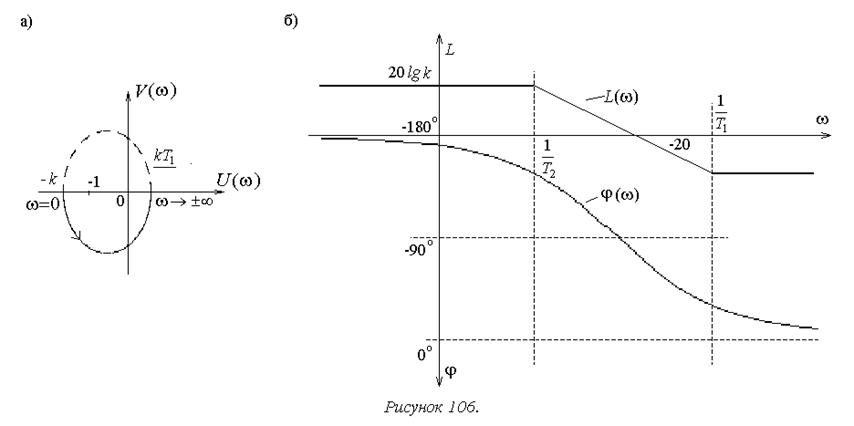
Рисунок 106 демонстрирует применение критерия Найквиста для замкнутой системы с единичной обратной связью при
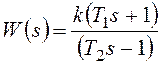 ,T1<T2.
,T1<T2.
На рисунке 106а представлена АФХ разомкнутой системы,
обеспечивающая устойчивость замкнутой системы. На рисунке 106б соответствующие
ей логарифмические частотные характеристики. Для рассматриваемого случая l=1 и на частоте, стремящейся к нулю, имеет место
положительный «полупереход» ЛФЧХ через горизонтальную ось, так как j(0)=-180°. Таким образом, для устойчивости замкнутой системы (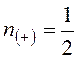 ,
, ![]() )
требуется, чтобы на малых частотах имело место L(w)>0, что будет при k>1. Это и есть условие устойчивости для рассматриваемой
системы.
)
требуется, чтобы на малых частотах имело место L(w)>0, что будет при k>1. Это и есть условие устойчивости для рассматриваемой
системы.
Для системы нейтрально устойчивой в разомкнутом состоянии с передаточной функцией
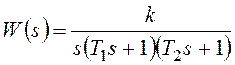
дополняющая
АФХ дуга бесконечно большого радиуса (рисунок 107а) для логарифмических
частотных характеристик превратится в отрезок прямой, дополняющий ЛФЧХ при ![]() , там, где
, там, где ![]() , от j(w)=0 до
, от j(w)=0 до 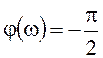 (рисунок
107б), так как нулевой корень здесь один.
(рисунок
107б), так как нулевой корень здесь один.
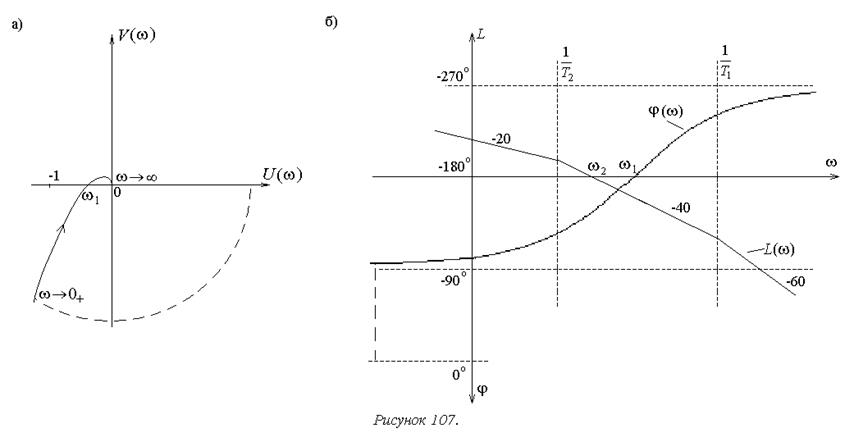
Для рассматриваемой системы l=0. Поэтому для устойчивости замкнутой системы
требуется, чтобы единственный – отрицательный – переход ЛФЧХ через горизонтальную
ось имел место за пределами участка, где L(w)>0. Тогда получим ![]() . В
результате приходим к условию, полученному ранее на основе АФХ: L(w1)<0
или
. В
результате приходим к условию, полученному ранее на основе АФХ: L(w1)<0
или ![]() , где
частота w1
определяется из условия
, где
частота w1
определяется из условия ![]() .
.
Для системы с передаточной функцией
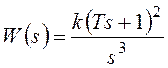
имеем
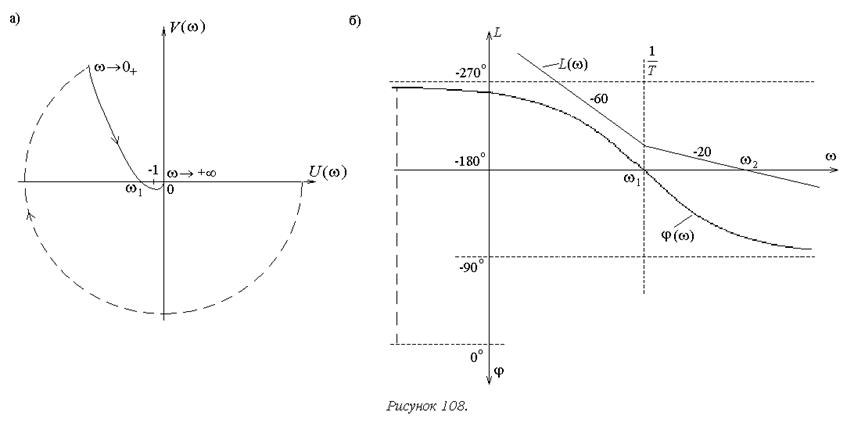
l=1, r=3. ЛФЧХ должна быть дополнена при ![]() отрезком от j(w)=0 до
отрезком от j(w)=0 до 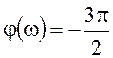 (рисунок 108б). Это дополнение обеспечивает
отрицательный переход ЛФЧХ через горизонтальную ось, который должен быть
скомпенсирован положительным. В результате приходим к условию, полученному
ранее на основе АФХ: L(w1)>0 или
(рисунок 108б). Это дополнение обеспечивает
отрицательный переход ЛФЧХ через горизонтальную ось, который должен быть
скомпенсирован положительным. В результате приходим к условию, полученному
ранее на основе АФХ: L(w1)>0 или ![]() , где частота w1
определяется из условия
, где частота w1
определяется из условия ![]() .
.
Для систем устойчивых и нейтрально устойчивых в
разомкнутом состоянии применение критерия Найквиста с использованием
логарифмических частотных характеристик может быть сведено к сравнению значений
двух частот, на которых характеристики пересекают
горизонтальную ось: w1 для ЛФЧХ
(![]() ) и w2 для ЛАХ
(L(w2)=0). Частоту w2 называют
частотой среза.
) и w2 для ЛАХ
(L(w2)=0). Частоту w2 называют
частотой среза.
Если ЛФЧХ пересекает горизонтальную ось снизу вверх (в отрицательном направлении), для устойчивости замкнутой системы достаточно выполнения неравенства w1>w2. Это условие абсолютной устойчивости замкнутой системы.
Если ЛФЧХ пересекает горизонтальную ось сверху вниз (в положительном направлении), получаем условие условной устойчивости замкнутой системы: w1<w2.
При совпадении w1 и w2 получаем колебательную границу устойчивости.
Важный практический интерес представляет вопрос о возможности использования для анализа устойчивости асимптотических ЛАХ, что в большинстве случаев значительно упрощает решение рассматриваемых задач.
Вспомним, что при отсутствии комплексных корней знаменателя передаточной функции погрешности асимптотической ЛАХ по отношению к точной достигают на сопрягающих частотах максимальных значений 3, 6 или 9 Дб в зависимости от изменения наклона асимптотической ЛАХ на конкретной частоте. При наличии комплексных корней погрешность на соответствующей сопрягающей частоте или на близкой к ней резонансной может достигать любых значений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.