Временные характеристики динамических звеньев и систем и способы их получения

Лекция 6.Временные характеристики динамических звеньев и систем и способы их получения

Рассмотренные выше формы моделей динамических звеньев и систем являются общими, то есть содержат всю информацию о динамических свойствах моделируемого объекта, необходимую для решения задач теории управления. В то же время эти формы нельзя признать наглядными с точки зрения понимания и анализа отдельных свойств. Эту роль выполняют временные и частотные характеристики звеньев и систем, получаемые на основе моделей в общих формах.

В теории управления рассматриваются две временные характеристики – переходная и весовая.

Переходная характеристика (переходная функция) – это реакция звена или системы на входной сигнал в виде единичной ступенчатой функции (рисунок 40).

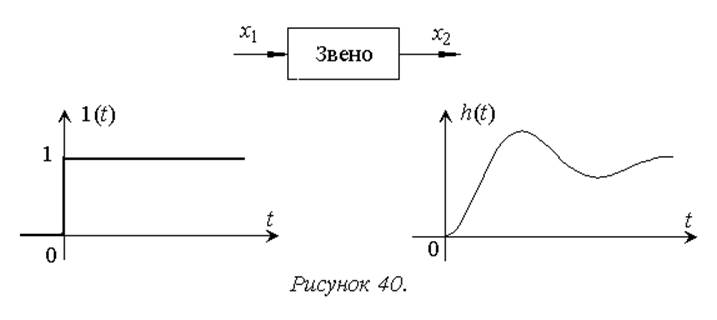
Рассмотрим основные способы (методы) получения переходной характеристики.

Классический метод – путем решения дифференциального уравнения звена или системы:

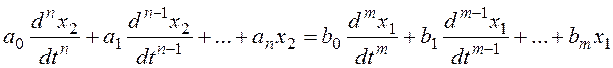
при нулевых начальных условиях.

В соответствии с определением переходной характеристики замене абстрактного входного сигнала x₁ на единичную ступенчатую функцию будет соответствовать замена x₂ на переходную характеристику (функцию):

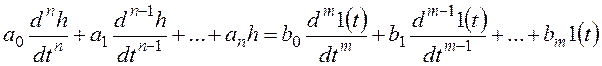
или

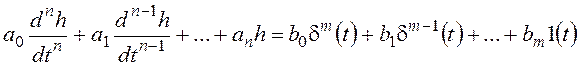, где .

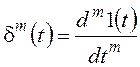Такая запись означает необходимость решения дифференциального уравнения

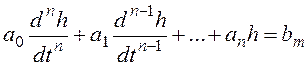
на интервале времени  с пересчетом заданных начальных условий «слева от нуля» в начальные условия «справа от нуля» с использованием коэффициентов при производных в правой части уравнения.

Решение линейного неоднородного дифференциального уравнения ищут в виде суммы двух составляющих:

, где h₀ – общее решение, h* – частное решение. В теории управления общее решение называют переходной составляющей, частное решение – вынужденной составляющей:

.

Переходную составляющую находят как решение однородного дифференциального уравнения:

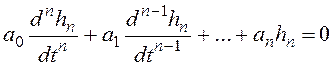
в форме суммы экспонент с произвольными коэффициентами. В показателях степени экспонент используются корни характеристического уравнения

.

Например, если все корни вещественные, причем кратные корни отсутствуют, переходная составляющая имеет вид:

.

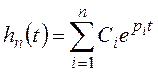Вынужденную составляющую находят в форме, соответствующей правой части. Если правая часть – константа, вынужденная составляющая – также константа, и для ее нахождения достаточно в уравнении положить производные равными нулю.

В качестве примера получим переходную характеристику апериодического звена 1-го порядка с уравнением: .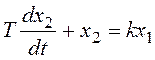

В соответствии со сказанным выше требуется решить уравнение

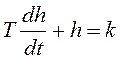
на интервале времени  при нулевых начальных условиях, причем благодаря отсутствию производных в правой части пересчет начальных условий не требуется.

Характеристическое уравнение здесь имеет вид:

и имеет один корень .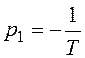

В результате получим выражение для переходной составляющей:

.

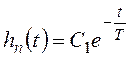Вынужденная составляющая здесь .

Результирующее полное решение уравнения:

.

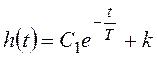Найдем C₁: ,  C₁= -k.

В результате получена переходная характеристика:

.

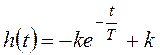Необходимо учесть, что в практических задачах переходные характеристики могут рассматриваться на различных временных интервалах. Для того, чтобы избавиться от необходимости отдельно указывать эту дополнительную информацию, выражения для переходных характеристик домножают на единичную ступенчатую функцию с соответствующим аргументом. Для рассматриваемого примера результат должен быть представлен в следующем виде:

.

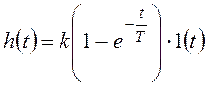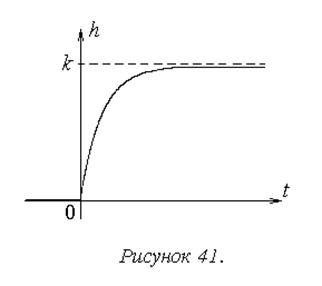
График переходной характеристики показан на рисунке 41.

Операторный метод – на основе передаточной функции звена или системы.

Данный метод следует рекомендовать прежде всего при наличии в правой части уравнения звена или системы производных, так как он не требует учета скачкообразного изменения начальных условий. В других случаях он так же, как правило, более удобен, чем классический.

Воспользуемся определениями передаточной функции и переходной характеристики с учетом известного изображения по Лапласу единичной ступенчатой функции :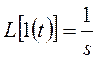

.

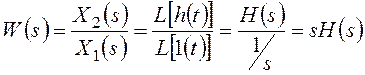Следовательно, при заданной передаточной функции изображение переходной характеристики можно найти по формуле:

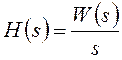.                                       (6.1)

После этого переходная характеристика может быть найдена путем перехода от изображения к оригиналу одним из следующих способов:

- непосредственно с помощью таблицы изображений – в простейших случаях;

- разложением H(s) на сумму табличных изображений;

- с помощью теорем разложения.

Найдем переходную характеристику дифференцирующего звена с замедлением.

Передаточная функция звена .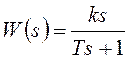

Найдем изображение переходной характеристики:

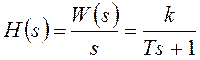
и воспользуемся следующей строкой из таблицы изображений.

Оригинал	Изображение

Преобразуем имеющееся изображение к табличному виду:

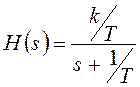
и с учетом линейности преобразования Лапласа получим искомую характеристику:

.

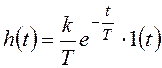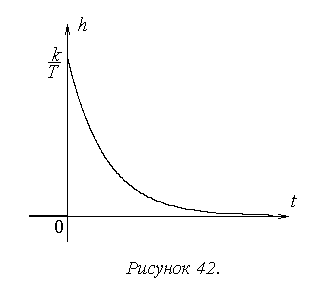
График переходной характеристики показан на рисунке 42.

Найдем переходную характеристику интегрирующего звена с замедлением.

Передаточная функция звена .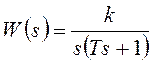

Найдем изображение переходной характеристики:

.

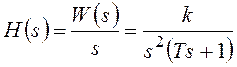Поскольку такое изображение в таблицах, как правило, отсутствует, разложим изображение на сумму:

.

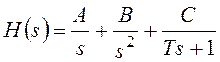Приведя разложение к общему знаменателю

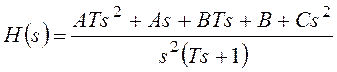
и приравняв числители полученного и исходного выражений, получим уравнения для коэффициентов:

AT+C=0,

A+BT=0,

B=k, откуда A= -kT, .

Слагаемые в разложении соответствуют следующим строкам таблицы изображений.

Оригинал	Изображение
1(t)

В результате получим:

.

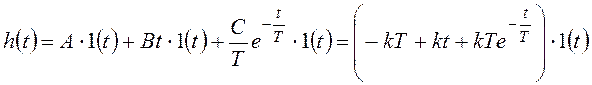Для построения характеристики сначала рассмотрим графики двух слагаемых полученного выражения, которые помогают получить итоговый график (рисунок 43).