Анализ свойств динамических звеньев по частотным характеристикам. Особые динамические звенья

Лекция 9.Анализ свойств динамических звеньев по частотным характеристикам. Особые динамические звенья

Динамические свойства звеньев и систем наглядно отражаются амплитудно-частотной и фазо-частотной характеристиками. Аналогичную информацию можно получить по логарифмическим частотным характеристикам.

Рассмотрим сначала АЧХ апериодического звена первого порядка 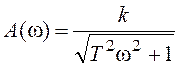 (рисунок 75).

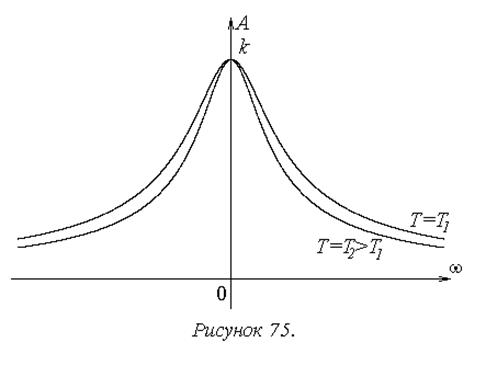
Основной вывод, к которому приводит анализ данной характеристики, состоит в том, что инерционность динамического звена приводит к ослаблению пропускаемых высокочастотных сигналов тем больше, чем выше степень инерционности, характеризуемая величиной постоянной времени.

Теперь рассмотрим семейство АЧХ типовых позиционных динамических звеньев (рисунок 76).

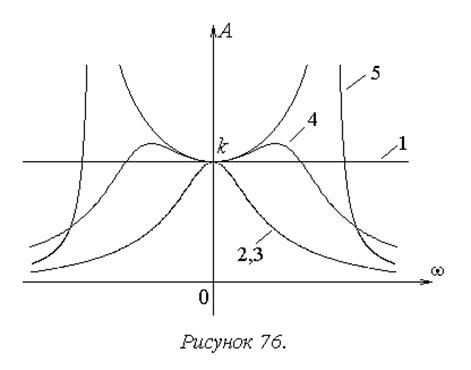
На основе их сравнительного анализа можно сделать следующие выводы:

1. Общее свойство звеньев данной группы – пропорциональность выходного сигнала входному – присуще идеальному звену данной группы, безынерционному (1), независимо от частоты входного сигнала.

2. Следствием инерционности остальных звеньев является ухудшение пропускания гармонических сигналов по мере увеличения их частоты. При этом в зависимости от характера инерционности это свойство проявляется по разному.

У апериодических звеньев 1-го (2) и 2-го порядка (3) степень ослабления гармонического сигнала растет монотонно.

У колебательного (4) и консервативного (5) звеньев этот же эффект наблюдается на частотах выше резонансной.

На рисунке 77 показано семейство АЧХ типовых интегрирующих динамических звеньев.

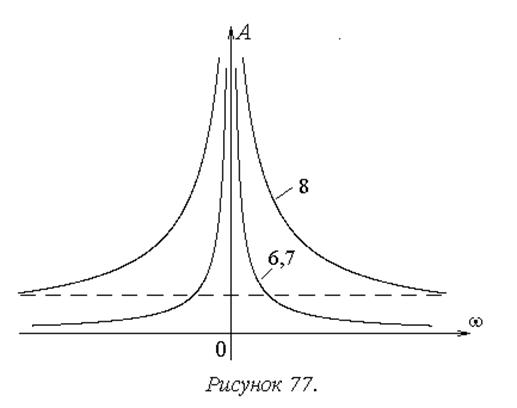
Общие свойства звеньев данной группы наглядно иллюстрируются АЧХ идеального интегрирующего (6) и интегрирующего с замедлением (7) звеньев – усиление сигналов низких частот и подавление высокочастотных сигналов. На высоких частотах проявляются плохие динамические свойства интегрирующих звеньев.

Улучшенные динамические свойства изодромного звена проявляются в том, что на низких частотах оно ведет себя как интегрирующее, усиливая низкочастотные сигналы, а на высоких – как безынерционное, сохраняя пропускную способность для высокочастотных сигналов.

Приведенные на рисунке 78 АЧХ типовых дифференцирующих звеньев показывают, что они обладают наилучшими динамическими свойствами по сравнению с двумя рассмотренными выше группами. Дифференцирующие звенья лучше пропускают высокочастотные сигналы, подавляя низкочастотные. Это в наибольшей степени характерно для идеального дифференцирующего звена (9). Инерционность дифференцирующего звена с замедлением (10) ограничивает возможности усиления высокочастотных сигналов.

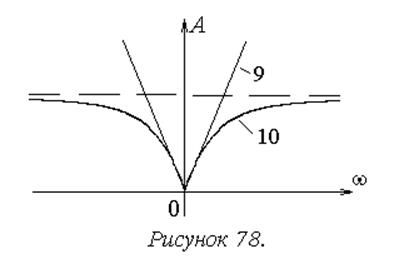
Следует отметить, что побочным отрицательным эффектом таких динамических свойств может быть низкая помехозащищенность систем, содержащих дифференцирующие звенья и подверженных влиянию шумовых (с ярко выраженной высокочастотной составляющей) помех.

Рассмотрим теперь фазо-частотные характеристики позиционных звеньев (рисунок 79).

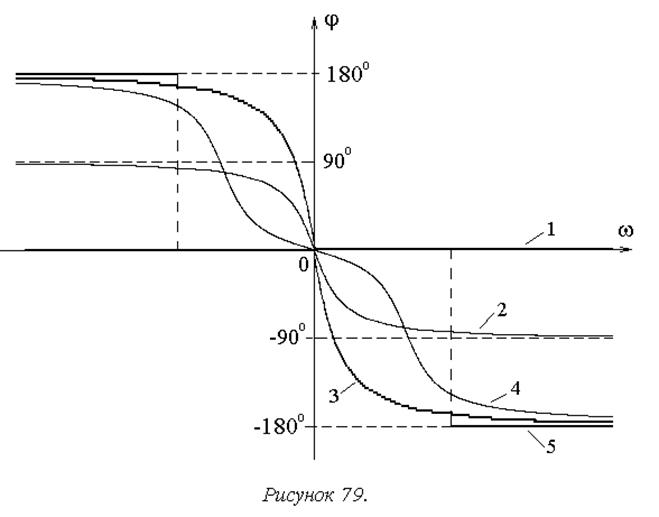
Общее свойство звеньев данной группы – масштабирование входного сигнала – не вызывает внесения фазового сдвига в преобразуемый сигнал, что и демонстрирует ФЧХ безынерционного звена (1). Инерционность остальных звеньев данной группы определяет отрицательный фазовый сдвиг, возрастающий с увеличением частоты. Порядок инерционности определяет диапазон изменения фазового сдвига: до -90° у апериодического звена 1-го порядка (2), до -180° у остальных звеньев данной группы.

Фазо-частотные характеристики интегрирующих звеньев показаны на рисунке 80.

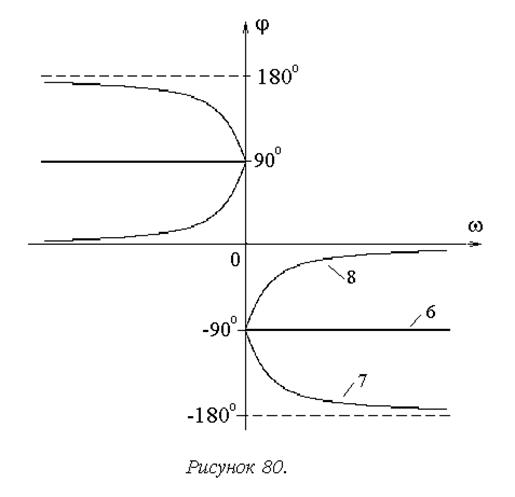
Все интегрирующие звенья вносят в преобразуемый сигнал отрицательный фазовый сдвиг, обусловленный выполняемой операцией интегрирования сигнала. Об этом непосредственно свидетельствует ФЧХ идеального интегрирующего звена (6). Инерционность интегрирующего звена с замедлением (7) определяет увеличение вносимого им отрицательного фазового сдвига по мере увеличения частоты преобразуемого сигнала. Улучшенные динамические свойства изодромного звена (8) здесь проявляются в форме снижения вносимого им отрицательного фазового сдвига по мере увеличения частоты.

Противоположные динамические свойства демонстрируют фазо-частотные характеристики дифференцирующих звеньев (рисунок 81).

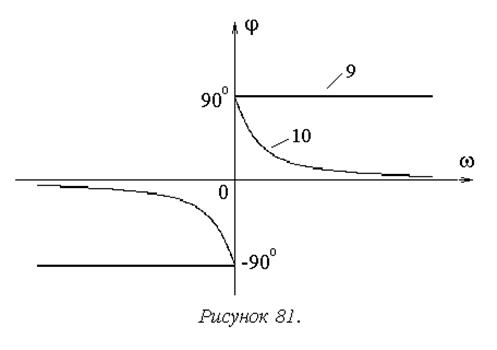
Выполняя операцию дифференцирования, звенья этой группы вносят в преобразуемый сигнал положительный фазовый сдвиг. Однократное дифференцирование (9) определяет фазовый сдвиг +90°. Инерционность дифференцирующего звена с замедлением (10) определяет снижение положительного фазового сдвига с увеличением частоты.

Рассмотренные примеры дают информацию для оценки динамических свойств более сложных звеньев.

К числу особых относятся прежде всего динамические звенья с запаздыванием. В дополнение к прочим динамическим свойствам для них характерно одно особое – реакция на любой входной сигнал начинает развиваться  не сразу после его поступления, а по истечении некоторого фиксированного интервала времени – времени запаздывания t_з.

Например, для апериодического звена 1-го порядка с запаздыванием, дифференциальное уравнение имеет вид:

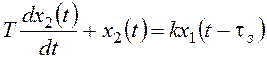, переходная характеристика показана на рисунке 82.

Очевидно, такая переходная характеристика может рассматриваться как реакция на единичную ступенчатую функцию. Следовательно, линейное динамическое звено с запаздыванием может быть представлено в виде последовательного соединения элемента запаздывания, обеспечивающего смещение входного сигнала во времени на величину -t_з, и обычного динамического звена.

Передаточная функция элемента запаздывания получается непосредственно на основе теоремы запаздывания для преобразования по Лапласу:

.

Переходная характеристика такого звена имеет вид h(t)=1(t-t_з).

Получим его частотные характеристики:

,

,

.

Следовательно, данное звено не изменяет амплитуду входного сигнала, но вносит отрицательный фазовый сдвиг, неограниченно возрастающий с увеличением частоты.

Рассматривая более широкий спектр динамических звеньев по сравнению с  типовыми, можно выделить группы звеньев с одинаковыми АЧХ и различными ФЧХ. Например, апериодическое звено 1-го порядка с 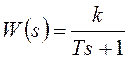 и неустойчивое апериодическое звено с 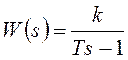. Для них АЧХ совпадают: , ФЧХ различаются:

- для апериодического звена 1-го порядка ,

- для неустойчивого апериодического звена .

Для передаточных функций более высокого порядка в такие группы могут входить по четыре и более звеньев. При этом всегда в состав группы входит звено, вносящее в преобразуемый сигнал минимальный фазовый          сдвиг. Такие звенья называют минимально-фазовыми. Отличительной особенностью минимально фазовых звеньев является отсутствие у числителя и знаменателя их передаточных функций    положительных вещественных корней или комплексных корней с положительной вещественной частью. Звенья, не отвечающие такому требованию, называют неминимально-фазовыми.