Построение областей устойчивости. Понятие о D-разбиении

Лекция 15.Построение областей устойчивости. Понятие о D-разбиении

Построение областей устойчивости и D-разбиение используются для исследования влияния значений параметров системы на ее устойчивость и качество.

Областью устойчивости в пространстве параметров системы (коэффициентов передачи, постоянных времени звеньев системы и др.) называется область значений параметров, при которых система является устойчивой.

Границы области устойчивости соответствуют границам устойчивости системы:

- апериодической (наличие нулевого корня характеристического полинома), получаемой по условию равенства нулю свободного члена характеристического полинома, a_n=0;

- соответствующей бесконечному корню характеристического полинома, получаемой по условию a₀=0;

- колебательной (наличие пары мнимых корней характеристического полинома), получаемой из условий D_n-1=0 в соответствии с критерием Гурвица, D(jw)=0 в соответствии с критерием Михайлова или W(jw)=-1 в соответствии с критерием Найквиста.

Практический интерес представляет построение области устойчивости в плоскости двух параметров, выбираемых из множества параметров системы в соответствии с особенностями решаемых задач. Основной способ ее построения предполагает использование критерия устойчивости Михайлова.

Вводится система координат 0AB, где по осям откладываются значения параметров системы А и В.

Коэффициенты характеристического полинома замкнутой системы

D(s)=a₀sⁿ+a₁s^n-1+…+a_n

выражаются через значения этих параметров.

Для получения уравнений границ области устойчивости составляются уравнения в соответствии с перечисленными выше условиями.

Основная трудоемкость при построении области устойчивости связана с построением кривой, соответствующей колебательной границе устойчивости. В соответствии с критерием Михайлова для ее получения составляется система уравнений:

,

, где X и Y– вещественная и мнимая части характеристического комплекса D(jw). Ее решение позволяет получить параметрические уравнения искомой кривой в форме A=A(w), B=B(w). Исключением из этих уравнений частоты можно получить уравнение в обычной форме B=B(A).

После нахождения границ области устойчивости определяется ее местонахождение. Для границ первого и третьего вида это можно сделать непосредственно на основе необходимого условия устойчивости. В области устойчивости должно иметь место a₀>0 и a_n>0.

Для колебательной границы рассматривается дополнительный критерий. Составляется определитель из частных производных

.

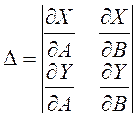Если D>0, то при движении вдоль этой границы в направлении увеличения частоты область устойчивости расположена слева. Если D<0 - справа.

Построенную область устойчивости принято выделять штриховкой, направленной внутрь.

В качестве примера построим область устойчивости для системы, представленной на рисунке 88, в плоскости параметров k и T₁.

Составим характеристический полином

D(s)=T₁T₂s³+(T₁+T₂)s²+s+k

и характеристический комплекс

.

Найдем границы устойчивости.

1. Апериодическая граница: a_n=k=0. Области устойчивости соответствует k>0.

2. Граница, соответствующая бесконечному корню: a₀=T₁T₂=0. В результате уравнение границы T₁=0. Области устойчивости соответствует T₁>0.

3. Колебательная граница:

,

.

В результате получим параметрические уравнения колебательной границы:

,

.

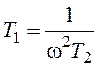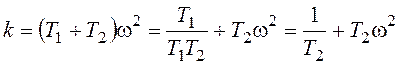Теперь исключим из полученных уравнений частоту:

.

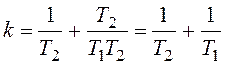Соответствующая кривая имеет вид гиперболы (рисунок 111).

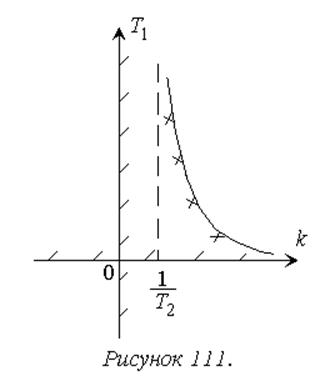
Найдем расположение области устойчивости относительно этой границы с учетом A=k, B=T₁:

.

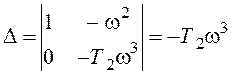При w>0 увеличению частоты от 0 до ∞ соответствует движение по колебательной границе, как следует из параметрических уравнений, в направлении увеличения k и уменьшения T₁. При этом D<0, то есть область устойчивости расположена справа.

При w<0 увеличению частоты от -∞ до 0 соответствует движение по колебательной границе, как следует из параметрических уравнений, в обратном направлении. При этом D>0, то есть область устойчивости расположена справа.

D-разбиением называется полная совокупность кривых, разбивающих плоскость параметров на области с различным распределением корней характеристического полинома D(s).