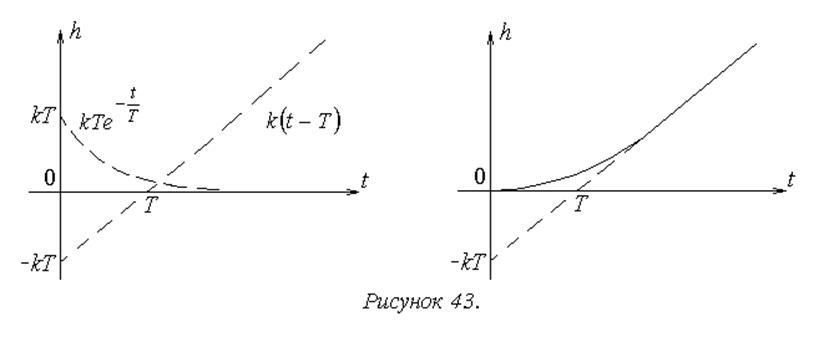
В наиболее сложных случаях для нахождения оригинала по изображению используют теоремы разложения.
Получение переходной функции интегрированием весовой характеристики.
Такая возможность является следствием (6.1) и свойств весовой характеристики, которые будут рассмотрены ниже.
Получение переходной функции на основе анализа преобразования звеном входного сигнала.
Данный способ удобен в ряде частных случаев и основан
на представлении звена или системы в виде последовательной или параллельной
цепи из простейших звеньев. Например, изодромное звено с передаточной функцией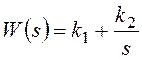 
может быть представлено параллельным соединением
безынерционного и идеального интегрирующего звеньев (рисунок 44).
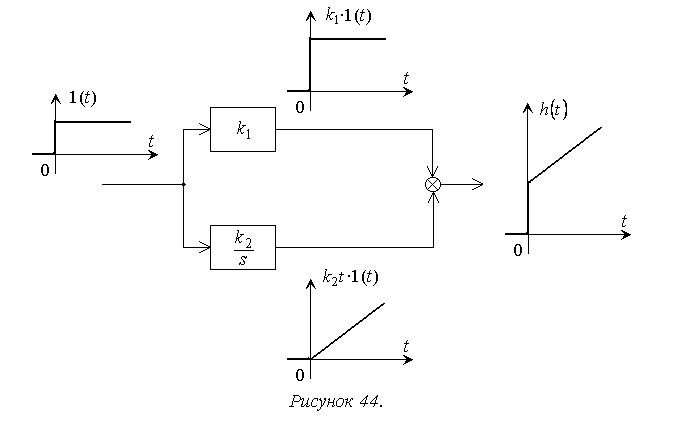
Первое звено масштабирует входной сигнал, второе интегрирует. Результирующая передаточная функция получается суммированием выходных сигналов этих звеньев:
.
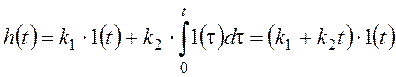Обсудим свойства звена или системы, которые отражает и позволяет анализировать переходная характеристика, на примере апериодического звена 1-го порядка. Полученная для него переходная характеристика (рисунок 41) показывает, что апериодическое звено 1-го порядка воспроизводит входной сигнал. Но это происходит с замедлением – по окончании переходного процесса. То есть данное звено характеризуется инерционностью.
На рисунке 45а показаны варианты этой же переходной характеристики для двух различных значений постоянной времени.
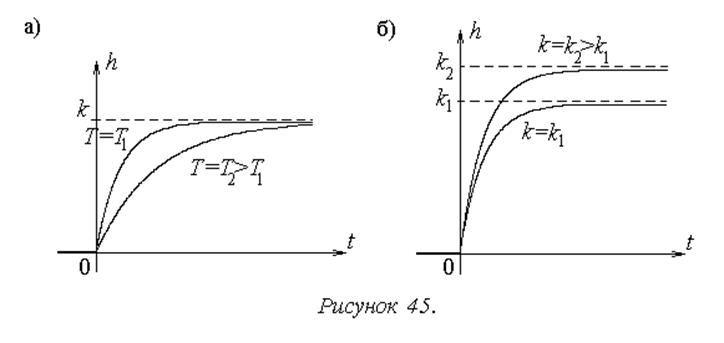
Таким образом, при увеличении значения постоянной времени переходный процесс замедляется. Постоянная времени характеризует инерционность динамического звена.
На рисунке 45б отображено влияние на процесс в звене коэффициента передачи.
Теперь проведем краткий анализ динамических свойств типовых звеньев, отражаемых переходной характеристикой.
На рисунке 46 показаны переходные характеристики типовых позиционных звеньев.
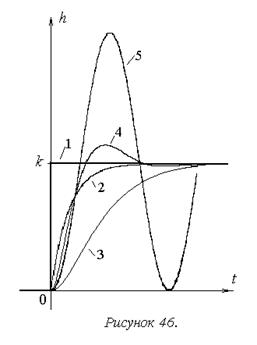
На основе их сравнительного анализа можно сделать следующие выводы:
1. Общим свойством звеньев данной группы является пропорциональность выходного сигнала входному, обеспечиваемая по окончании переходного процесса. Именно это свойство является единственным для идеального звена данной группы – безынерционного (1).
2. Общее отличие всех звеньев от безынерционного состоит в наличии переходного процесса, вызванном их инерционностью. Различия же между звеньями внутри группы определяются количеством и соотношением постоянных времени, то есть характером инерционности.
Так процесс в звеньях второго порядка – апериодическом 2-го порядка (3), колебательном (4) и консервативном(5) – в отличие от апериодического звена 1-го порядка (2), начинает развиваться не мгновенно, так как здесь и начальная скорость изменения сигнала – нулевая.
Кроме того, в зависимости от соотношения постоянных времени у звеньев второго порядка наблюдается различный характер процесса.
Динамические свойства, отражаемые переходной характеристикой, определили названия типовых динамических звеньев.
На рисунке 47 показаны переходные характеристики типовых интегрирующих звеньев.
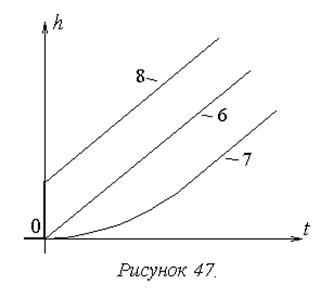
На основе их сравнительного анализа можно сделать следующие выводы:
1. Общее свойство звеньев данной группы отражается характеристикой идеального интегрирующего звена (6) – в установившемся процессе выходной сигнал пропорционален интегралу входного.
2. У остальных звеньев данной группы проявляются дополнительные динамически свойства: инерционность у интегрирующего звена с замедлением (7) и противоположный эффект у изодромного звена (8), приводящий к тому, что процесс в данном звене ускоряется по сравнению с процессом в идеальном звене. Формально такая разница в динамических свойствах отражается расположением постоянной времени в передаточной функции: в знаменателе при наличии инерционности и в числителе в противоположном случае.
На рисунке 48 показаны переходные характеристики типовых дифференцирующих звеньев.
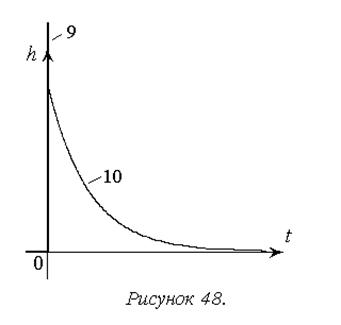
На основе их сравнительного анализа можно сделать следующие выводы:
1. Общее свойство звеньев данной группы отражается характеристикой идеального дифференцирующего звена (9) – в установившемся процессе выходной сигнал пропорционален производной входного.
2. Наличие инерционности у дифференцирующего звена с замедлением (10) приводит к переходному процессу.
Весовая характеристика (весовая функция, функция веса) – это реакция звена или системы на входной сигнал в виде d-функции (функции Дирака).
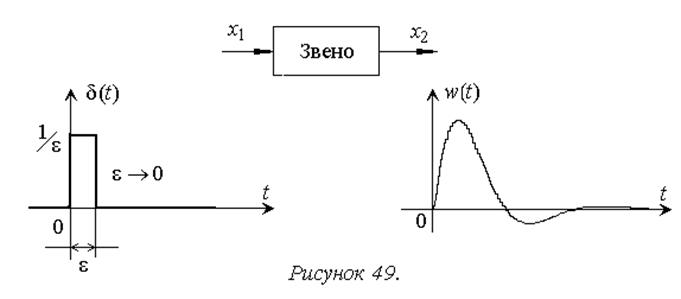
Вспомним основные свойства d-функции:
, 
, 
.
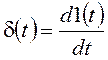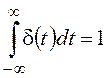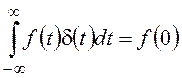Рассмотрим наиболее удобные способы (методы) получения весовой характеристики.
Операторный метод.
Воспользуемся определениями передаточной функции и
весовой характеристики с учетом известного изображения по Лапласу d-функции 
:
.
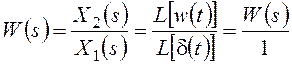Следовательно, передаточная функция является изображением по Лапласу функции веса.
Найдем весовую характеристику апериодического звена 1-го порядка.
Преобразуем передаточную функцию звена к табличному виду
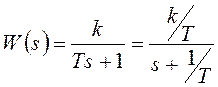
и запишем результат:
.
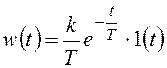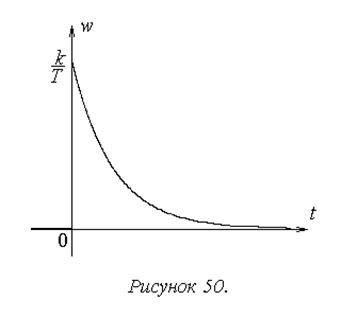
График весовой характеристики показан на рисунке 50.
Получение весовой функции дифференцированием переходной характеристики.
Следствием полученного выше соотношения 
является следующая
связь между весовой и переходной функциями:
.
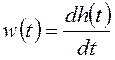Вернемся к последнему примеру.
Переходная характеристика апериодического звена 1-го порядка была получена выше:
.
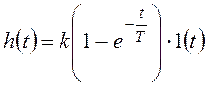Продифференцируем ее:
.
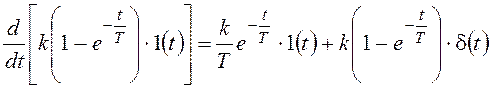С учетом тождественного равенства нулю d-функции при всех 
упростим
полученное выражение:
.
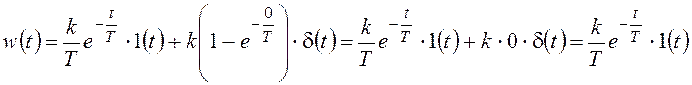Получение весовой функции на основе анализа преобразования звеном входного сигнала - способ аналогичен получению переходной функции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.