Указанные значения погрешностей достаточно велики для того, чтобы использование асимптотической ЛАХ в ряде случаев приводило к получению неверных результатов анализа устойчивости, как количественно, так и качественно.
Здесь следует учесть, что по мере удаления от сопрягающей частоты влево или вправо погрешность асимптотической ЛАХ снижается: на расстоянии 0,3 декады от сопрягающей частоты она уменьшится примерно в 3 раза, на расстоянии 0,5 декады от сопрягающей частоты – более, чем в 7 раз.
Поэтому общая рекомендация по вопросу о возможности использования асимптотических ЛАХ для анализа устойчивости сводится к следующему: в тех случаях, когда частоты w1 и w2, с которыми связаны основные расчеты, оказываются на расстоянии менее 0,3 декады от сопрягающих частот, требуется уточнение результатов расчета на основе точных выражений для ЛАХ или АЧХ.
Критерий устойчивости Найквиста является основой для определения показателей качества системы: запасов устойчивости по амплитуде и по фазе.
Запас устойчивости по амплитуде La показывает, во сколько раз нужно изменить коэффициент передачи разомкнутой системы, чтобы перевести устойчивую замкнутую систему на границу устойчивости.
Запас устойчивости по амплитуде может быть определен по АФХ (рисунок 109) или логарифмическим частотным характеристикам разомкнутой системы.
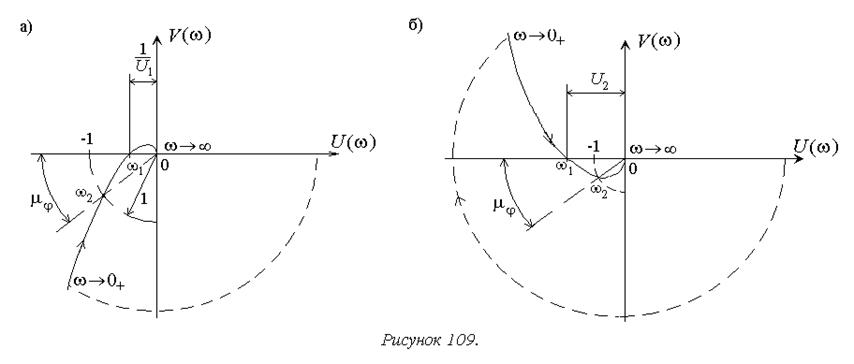
Запас устойчивости по амплитуде чаще всего выражают в децибелах.
Для абсолютно устойчивой
системы (рисунок 109а) La показывает, во сколько раз нужно увеличить
коэффициент передачи для достижения границы устойчивости: ![]() , где
, где 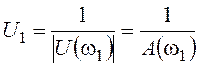 , а
частота w1
определяется по условию
, а
частота w1
определяется по условию ![]() или
или ![]() .
.
Для условно устойчивой
системы (рисунок 109б) La показывает, во сколько раз нужно уменьшить коэффициент
передачи для достижения границы устойчивости: ![]() , где
, где ![]() , а частота w1 определяется из тех же соображений.
, а частота w1 определяется из тех же соображений.
Запас устойчивости по фазе mj показывает, какой по абсолютной величине дополнительный
отрицательный фазовый сдвиг нужно добавить к фазовому сдвигу, обеспечиваемому
разомкнутой системой, чтобы перевести устойчивую замкнутую систему на границу
устойчивости. В соответствии с этим определением графически по АФХ запас по
фазе может быть найден как угол между отрицательной вещественной полуосью и
прямой, проведенной из начала координат в точку пересечения АФХ с окружностью
единичного радиуса. Именно на такой угол нужно повернуть АФХ, чтобы она
пересекла горизонтальную ось в точке (-1; 0j), что
соответствует границе устойчивости. Этот угол может быть найден по соотношению:
![]() , где w2 –
частота среза, определяемая по условию
, где w2 –
частота среза, определяемая по условию ![]() .
.
Следствием вышесказанного с
учетом соотношения ![]() является способ определения запасов
устойчивости по амплитуде и фазе по логарифмическим частотным характеристикам:
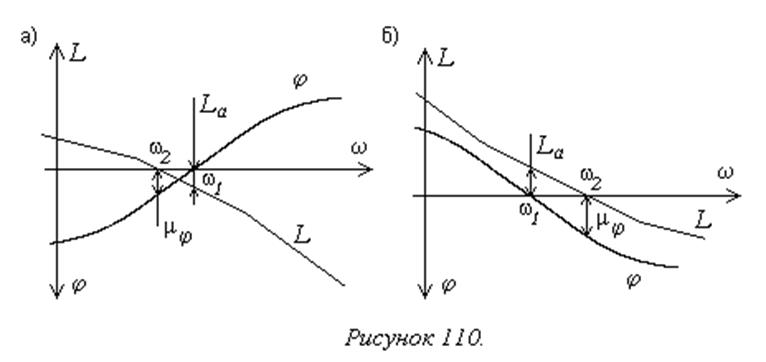
на рисунке 110а для абсолютно устойчивой, на рисунке 110б для условно
устойчивой системы.
является способ определения запасов
устойчивости по амплитуде и фазе по логарифмическим частотным характеристикам:
на рисунке 110а для абсолютно устойчивой, на рисунке 110б для условно
устойчивой системы.
В качестве примера проанализируем устойчивость замкнутой системы с единичной отрицательной обратной связью по заданной асимптотической ЛАХ разомкнутой системы.
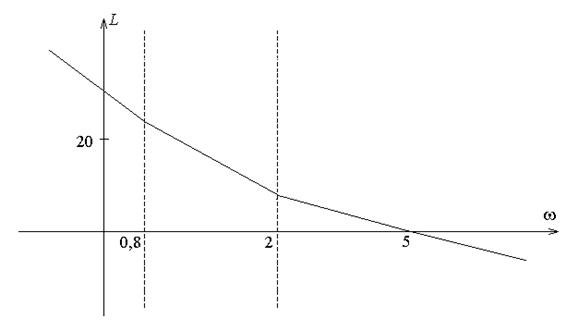
По асимптотической ЛАХ с учетом заданных масштабов восстанавливаем передаточную функцию разомкнутой системы:

и значения параметров T1=1,25; T2=0,5.
Наклоны участков асимптотической ЛАХ: -60; -40; -20 Дб/дек.
Теперь найдем опорную точку первого участка асимптотической ЛАХ и рассчитаем коэффициент передачи разомкнутой системы: Lас(2)=8Дб; Lас(0,8)=24Дб. Координаты опорной точки: w=1, L(1)(1)=18Дб. Из уравнения 20lgk=18 найдем k=8.
Для системы третьего порядка анализ устойчивости проще всего выполнять с помощью критерия Гурвица. Составим характеристический полином и требуемый определитель Гурвица:
D(s)= s3+kT1T2s2+k(T1+T2)s+k,
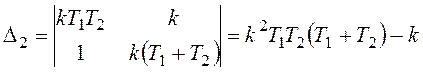 .
.
Подстановка в определитель количественных данных задачи позволяет сделать вывод об устойчивости системы.
![]() .
.
Теперь найдем условие устойчивости:
![]() ,
,
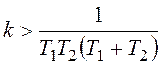 , из которого следует, что система условно устойчива.
, из которого следует, что система условно устойчива.
Найдем критический коэффициент передачи
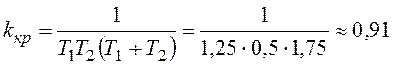 , и запас устойчивости по амплитуде:
, и запас устойчивости по амплитуде:
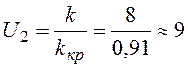 ,
,
![]() .
.
Получим выражение для ФЧХ:
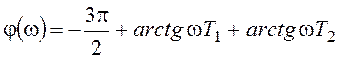 , и с учетом известной частоты среза,
удаленной более, чем на 0,3 декады от ближайшей сопрягающей частоты, найдем запас устойчивости по фазе:
, и с учетом известной частоты среза,
удаленной более, чем на 0,3 декады от ближайшей сопрягающей частоты, найдем запас устойчивости по фазе:
![]() ,
,
![]() .
.
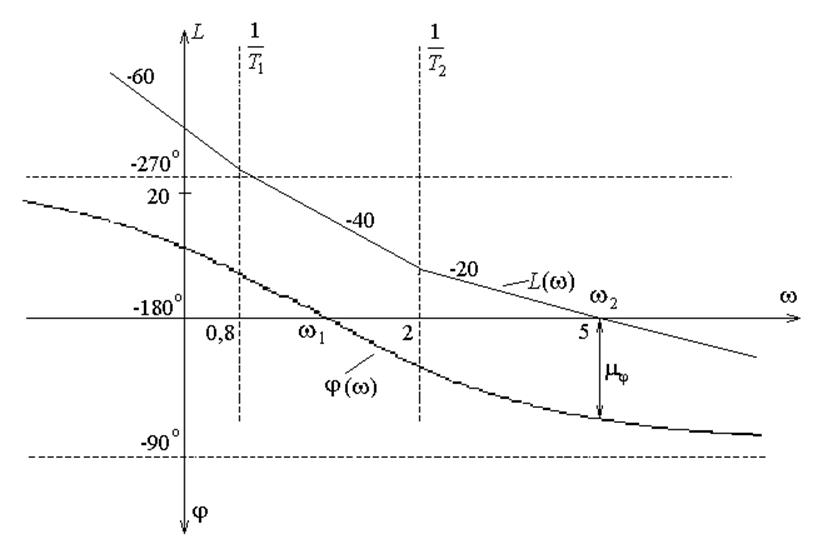
Полностью логарифмические характеристики представлены на рисунке.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.