




















Вопросы к экзамену по курсу
«ОСНОВЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ»
1. Обобщенная схема ЦОС. Дискретизация аналогового сигнала. Основная полоса частот.
2. Математический аппарат описания дискретных сигнала и систем. Дискретные преобразования Фурье, Лапласа Z-преобразование.
3. Z-преобразование. Отображение p-плоскости на Z-плоскости. Основные свойства Z-преобразования.
4. Обратное Z-преобразование. Способы вычисления обратного Z-преобразования.
5. Описание линейных дискретных систем во временной области. Формула свертки. Разностное уравнение.
6. Рекурсивные и перекурсивные линейные дискретные системы. Импульсная характеристика рекурсивных и перекурсивных линейных дискретных систем.
7. Устойчивость линейных дискретных систем. Оценка устойчивости по импульсной характеристики.
8. Описание линейных дискретных систем в Z-области. Понятие передаточной функции.
9. Оценка устойчивости линейных дискретных систем по передаточной функции.
10.Описание линейных дискретных систем в частотной области. Понятие частотной характеристики (ЧХ). Связь ЧХ с передаточной функцией.
11.Свойства частотных характеристик. Расчет амплитудно-частотной и фазо-частотной характеристик.
12.Прямая структура линейной дискретной системы.
13.Каскадная структура линейной дискретной системы.
14.Параллельная структура линейной дискретной системы.
15.Прямая каноническая структура ЛДС 1.
16.Каноническая структура ЛДС 2.
17.Каноническая структура ЛДС 3.
18.Спектральный анализ. Спектр дискретного сигнала. Дискретное преобразование Фурье.
19.Свойства дискретного преобразования Фурье.
20.Алгоритм быстрого преобразования Фурье с прореживанием по времени.
21.Алгоритм быстрого преобразования Фурье с прореживанием по частоте.
22.Вычисление обратного дискретного преобразования Фурье с помощью алгоритма БПФ.
23.Оценка выигрыша в количестве операции при вычислении дискретного преобразования Фурье с помощью алгоритма БПФ с основанием 2.
24.Задание требований к цифровым фильтрам на примере избирательных фильтров.
25.Характеристика задачи оптимального синтеза цифрового фильтра.
26.Мера близости в задачах аппроксимации цифровой обработки сигналов. Чебышевская мера.
27.Мера близости в задачах аппроксимации цифровой обработки сигналов. Среднеквадратическая мера.
28.Постановка задачи оптимального синтеза цифровых фильтров. Весовая функция.
29.Процедура решения задачи оптимального синтеза цифрового фильтра.
30.Понятие о полиномах Чебышева.
31.Полиномиальный алгоритм Ремеза.
32.Синтез КИХ-фильтров. Условия безыскаженной передачи.
33.Квантование чисел и сигналов.
34.Модели процессов квантования.
35.Шум аналого-цифрового преобразования.
36.Шум АЦП, приведенный к выходу цифровой системы.
37.Учет шумов квантования в прямой форме цифрового фильтра.
38.Учет шумов квантования в канонической форме цифрового фильтра.
ПРИЛОЖЕНИЕ 12.1
П. Пример использования метода стандартного Z-преобразования (инвариантности ЧХ)
Используем в качестве аналога-прототипа полосовой фильтр с передаточной функцией, описываемой выражением:
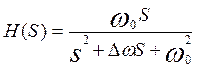 , (п.1)
, (п.1)
где w0=2p¦0 (¦0 – резонансная частота), Dw=2pD¦=2p¦0 /Q
(Dw - полоса пропускания на уровне 0,7, Q – добротность)
Пример Q=4, тогда
Особые точки этой передаточной функции имеют следующие координаты:
нуль: S0=0
полосы: Sn1,2=-w0/8±jw0(Ö63/8), (п.2)
Представим передаточную функцию в виде …..
![]()
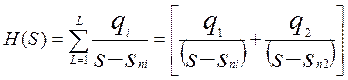 ,
(п.3)
,
(п.3)
где qi – вычеты комплексной функции H(S) в каждом из полюсов Sni, которые определил по формуле определение вычета в заданном полюсе [см. (п. )
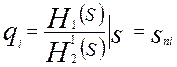 , где
, где
![]() (S) – первая производная по S.
(S) – первая производная по S.
Тогда величины q1 и q2 принимаю значения
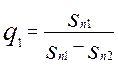 ;
; 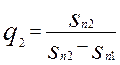 , (п. 4)
, (п. 4)
Как было установлено ранее, аналогом соотношения (п.3) является в Z-плоскости равенство [см. п.3.5.3]
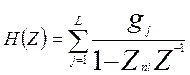 , (п.5)
, (п.5)
где полосы функции H(Z)
![]() , (п.6)
, (п.6)
Из сравнения выражений (п.3) и (п.5) видно, что для получения передаточной функции H(Z) БИХ-фильтра необходимо в выражении для H(S) провести замену
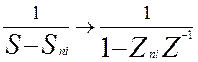 (п.7)
(п.7)
Используя в выражении (п.3) замену (п.7), получим исходную запись передаточной функции рассчитываемого БИХ-фильтра:
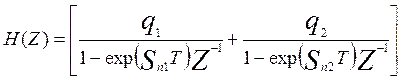 , (п.8)
, (п.8)
Подставив формулы (п.4) в (п.8) и выполнив необходимые преобразования, получим выражение для передаточной функции БИХ-фильтра в окончательном виде:
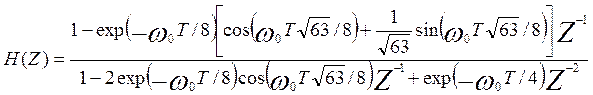 , (п.9)
, (п.9)
Примерный вид АЧХ такого фильтра изображен на рисунке П.1 при ¦0=10кГц
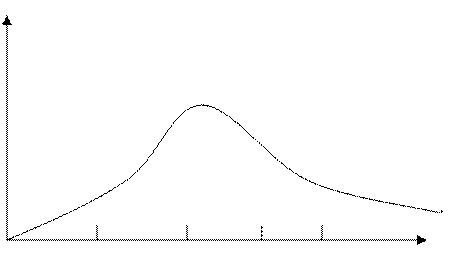 1 - ¦д – 150
кГц
1 - ¦д – 150
кГц
2 - ¦д – 100 кГц
3 - ¦д – 50 кГц
Рисунок П.1
В заключение отметим, что метод стандартного Z-преобразования неприменим в случае, когда в передаточной функции аналога-прототипа число нулей равно или больше числа полюсов [из-за невозможности представления H(Z) в виде суммы (п.5)]. Такой случай имеет место при синтезе ФВЧ и РФ.
ПРИЛОЖЕНИЕ 12.2
Применим метод билинейного Z-преобразования для расчета полосового БИХ-фильтра, имеющего передаточную функцию аналогового прототипа
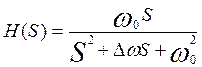 , (п.1)
, (п.1)
Учитывая свойство билинейного Z-преобразования, необходимо осуществить предыскажение аналога-прототипа с помощью частотно-преобразующей функции
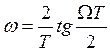 , (п.2)
, (п.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.