Практикум по курсу "Основы цифровой обработки сигналов"

Практикум по курсу

«ОСНОВЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ»

Практикум к разделам 1,2.

Задача 1.Сигнал  дискретизируется с шагом с. Что представляет собой дискретизированный сигнал ?

Решение:

Воспользуемся понятием нормированной круговой частоты. Тогда дискредитированный сигнал можно описать выражением

 .

Поскольку

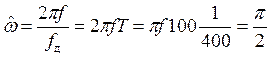 , окончательно запишем

  .

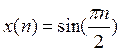Задача 2.Последовательность 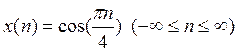 получена в результате дискретизации непрерывного сигнала  с частотой 1 кГц. Необходимо найти значения частоты , при которых такое возможно.

Решение:

Вновь воспользуемся понятием нормированной круговой частоты, что приводит к соотношению

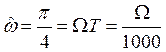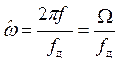, , откуда

.

Является ли это решение единственным? Из курса тригонометрии мы знаем, что

, тогда второе решение получим из равенства

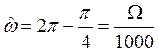 ,  или  .

Корректно ли такое решение? (См. след. задачу)

Во втором случае

т.е. некорректно.

Задача 3. Непрерывный сигнал  дискретизируется с шагом T, в результате чего получается последовательность 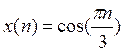. Необходимо определить:

а) значение Т, согласованное с условием задачи;

б) единственное ли это решение.

Решение:

По аналогии с вышеприведённым рассуждением находим два значения периода дискретизации Т:

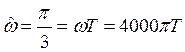, откуда

  или

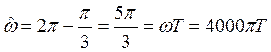,откуда

  или 

В соответствии с теоремой Котельникова, необходимо выполнение условия .

По условиям задачи .

Как видим, во втором случае условие теоремы Котельникова не выполняется, т.е. решение некорректно.

Задача 4.  Найдите Фурье-образ последовательности

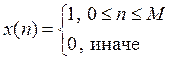
Решение:

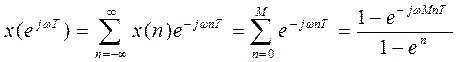
P.S. Использовалась формула суммы М-членов геометрической прогрессии 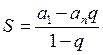, где

-первый член прогрессии

  - М-й член прогрессии

  - знаменатель прогрессии.

Практикум к разделу 3.

Задача 1. Вычислить Z-преобразование последовательности

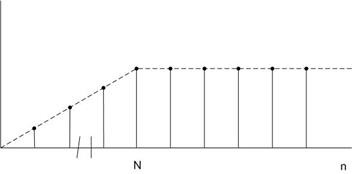
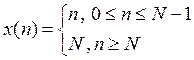
Решение :

Запишем

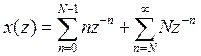    (п.3.1)

Второе слагаемое представим в виде

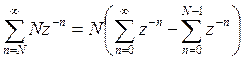     (п.3.2)

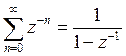    - в соответствии с таблицей соответствия

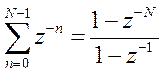  - сумма членов конечной геометрической прогрессии

Подставляя два последних соотношения в (п.3.2), получим

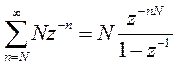
Первое слагаемое также преобразуем к виду

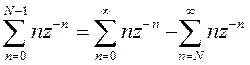   (п.3.3)

Для нахождения Z-преобразования второго слагаемого в (п.3.3) воспользуемся свойством производной Z-преобразования, которая утверждает, что если , то

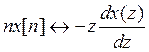
Доказательство получается с помощью дифференцирования равенства  ,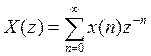

.

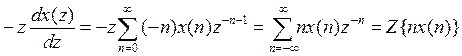Свойство производной, приложенное к нашей задаче, даёт  , -ед.скачок

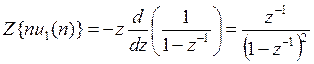
Таким образом

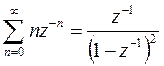
Тогда в соответствии с теоремой о задержке

.

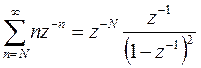Подставляя два последних соотношения в (п.3.3), получим

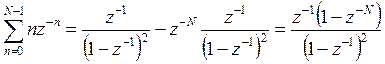  (п.3.4)

Подставляя (п.3.3) и (п.3.4) в (п.3.1), окончательно получаем:

.

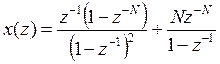Задача 2.  Восстановить последовательность по её  Z-преобразованию:

Решение:

Перемножив входящие в условие задачи сомножители, получим произведение

Используя таблицы соответствия, получим исходную последовательность

.

Задача 3. Найти последовательность (оригинал) по известному  Z-изображению, используя теорему Коши о вычетах

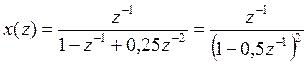
Решение:

Z- изображение представляет собой дробно-рациональную функцию второго порядка, имеющую вещественный полюс  кратности (т.е. два одинаковых полюса). Поэтому решения будем искать в виде суммы вычетов:

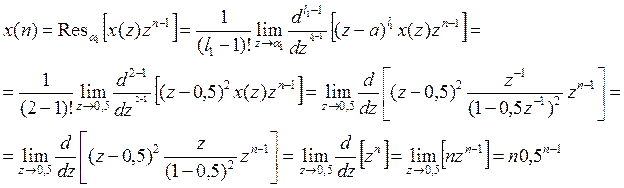
Задача 4.  Найти оригинал по известному Z- изображению, используя формулу, полученную через разложение в ряд Лорана

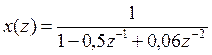
Решение:

Z- изображение представляет собой дробно-рациональную функцию второго порядка, которую можно представить в виде

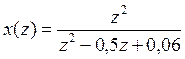
И которая имеет два простых вещественных полюса  и . Следовательно, имеем два вычета. Вычет в полюсе   равен

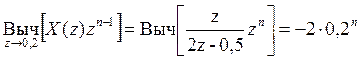
Т.к. 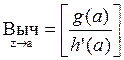, где ;

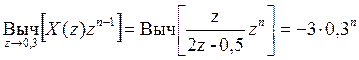
Тогда

.

Аналогичный результат получится и по другой формуле:

.

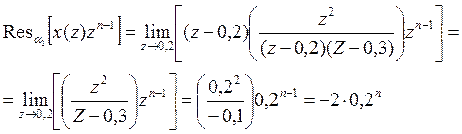
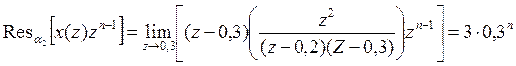
Задача 5.  (Лучше начинать с неё)  Определить Z-преобразование последовательности

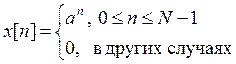
Решение: 

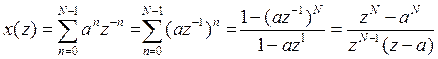
P.S. Использовалась формула суммы первых М-членов геометрической прогрессии 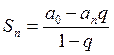, где

- знаменатель прогрессии,

.

Практикум к разделам 4,5.

Задача 1.  Рассмотрим ЛДС, пара сигнал-отклик которой удовлетворяет разностному уравнению:

      

Необходимо найти карту нулей и полюсов её передаточной функции, а также определить импульсную характеристику этой системы.

Решение:

Перейдём из временной в Z-область, что преобразует РУ к виду

Тогда для передаточной фукции будет справедливо соотношение

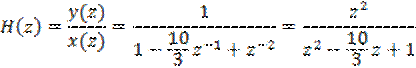
Нулями ПФ будут соответствовать значения . Полюсам ПФ соответствуют:

;    ;    =1/3

Для нахождения ИХ разложим ПФ на дроби (простые):

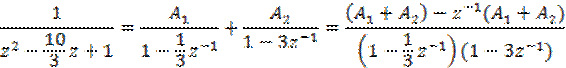
Откуда определяем коэффициенты :

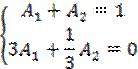
Решение этой системы:     ,   , следовательно ПФ принимает вид:

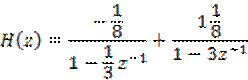
Используя таблицу соответствия, получим ИХ:

Задача 2.  Дана ЛДС, описывающаяся линейным разностным уравнением с постоянными коэффициентами и с нулевыми начальными условиями. Известно, что реакция на единичный скачок этой системы имеет вид:

Необходимо определить:

А) разностное уравнение, описывающее данную ЛДС;

Б) импульсную характеристику;

В) является ли данная система устойчивой

Решение:

Найдём передаточную функцию ЛДС, для чего определим Z-преобразования входного воздействия и реакции.

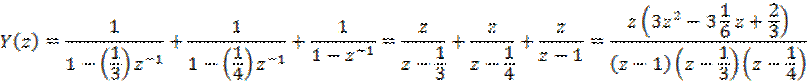
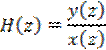
Откуда

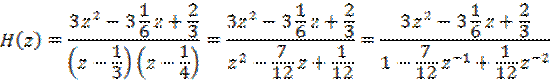
Полюсы данной ПФ :    ;  =1/4 . Система устойчива, поскольку полюсы находятся внутри окружности единичного радиуса.

Разностное уравнение, описывающее данную ЛДС имеет вид:

 .

Поделив числитель на знаменатель ПФ, получим:

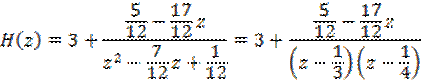
Воспользуемся методом разложения ПФ на элементарный дроби, в соответствии с которым можно записать ПФ в виде:

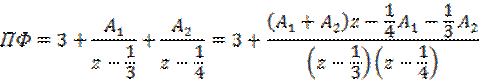
Откуда

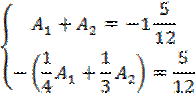
Решение последней системы даёт решение:     ,    .

Тогда ПФ принимает окончательный вид:

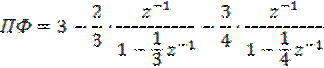
Этой ПФ соответствует ИХ

  , где  и  - единичная функция и функция единичного скачка соответственно.

Практикум к разделу 6

Задача 1.  Для каждой из следующих систем определите, является ли она:

1)  Устойчивой

2)  Линейной

3)  Стационарной

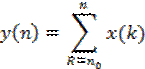
Ответ:

Устойчива, линейна, стационарна.