Задача 6. Требуется дискретизировать непрерывный сигнал, содержащий компоненты с частотами 1кГц и 2 кГц следующего вида:
![]() (1)
(1)
А затем выполнить 8-точеченое ДПФ этого сигнала.
Решение:
Основная (экспоненциальная) форма ДПФ имеет вид:
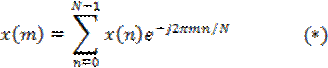
Из
тождества Эйлера ![]() можно получить эквивалентную тригонометрическую
форму ДПФ
можно получить эквивалентную тригонометрическую
форму ДПФ
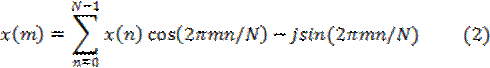
Где
![]() – m-й компонент ДПФ, т.е. x(0), x(1),…,x(N-1) в частотной
области
– m-й компонент ДПФ, т.е. x(0), x(1),…,x(N-1) в частотной
области
![]() – последовательность входных отсчетов, n=0, 1,…, N-1
– последовательность входных отсчетов, n=0, 1,…, N-1
При
частоте дискретизации![]() мы берем отсчеты входного сигнала каждые
мы берем отсчеты входного сигнала каждые ![]() секунд. Поскольку N=8 нам нужно
взять 8 входных отсчетов, над которыми выполнить ДПФ. Таким образом, 8 элементная
последовательность x(n) определяется как
секунд. Поскольку N=8 нам нужно
взять 8 входных отсчетов, над которыми выполнить ДПФ. Таким образом, 8 элементная
последовательность x(n) определяется как
![]()
Если
мы выберем частоту дискретизации ![]() , то значит этих отсчетов равны
, то значит этих отсчетов равны
![]()
![]()
Подставляя
значения отсчетов в ![]() в формулу (2), получаем
в формулу (2), получаем
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Итак
мы видим, что входной сигнал ![]() содержит компонент с частотой 1 кГц,(n=1) (т.к.
содержит компонент с частотой 1 кГц,(n=1) (т.к. ![]() ) с амплитудой
) с амплитудой
![]()
Повторяя проделанные вычисления для n=2,…,7, получаем
![]()
![]()
![]()
![]()
![]()
![]()
Наконец, определим x(0)
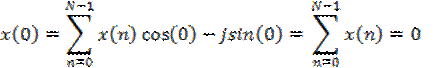
Точный спектральный анализ дает рис.1, из которого видно, что x(t) имеет с частотой 1кГц (n=1) и 2кГц (m=2). Более того, амплитуда тока с частотой 1кГц в два раза больше, чем амплитуда тока с частотой 2кГц.
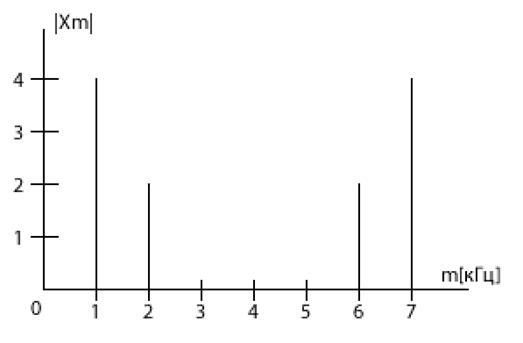
Рисунок 1
Все это мы могли понять и непосредственно из формулы (1). Однако наблюдательный студент может задать вопрос. Что означают ненулевые значения амплитуды при m=6 и m=7? Это связано с так называемым свойством симметрии ДПФ. А именно, m-й отсчет ДПФ имеет такой же модуль, что и (N-m)-й. Действительно, подставляя в формулу (*) (N-m) вместо m, получаем
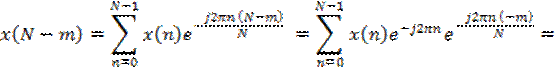
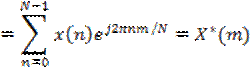
Т.к.![]() , * - знак комплексного сопряжения (на модуль не
влияет).
, * - знак комплексного сопряжения (на модуль не
влияет).
Таким
образом, чтобы получить ДПФ (вернее модуль ДПФ) достаточно вычислить только
первые N/2+1 отчетов X(m) при ![]() . Отсчетом X(N/2+1) до X(N-1) не дают
дополнительной информации о модуле спектральных составляющих последовательности
X(n). (P.S. Свойство
симметрии справедливо лишь при подаче на вход вещественных значений входных
величин. При подаче комплексных значений это свойство не выполняется).
. Отсчетом X(N/2+1) до X(N-1) не дают
дополнительной информации о модуле спектральных составляющих последовательности
X(n). (P.S. Свойство
симметрии справедливо лишь при подаче на вход вещественных значений входных
величин. При подаче комплексных значений это свойство не выполняется).
Задача
7. Вычислить
8-точечную БПФ последовательности данных, представляющую сигнал ![]() из
предыдущей задачи.
из
предыдущей задачи.
Решение: В соответствии с задачей 3 дискретная последовательность имеет вид
![]()
![]()
Полная реализация алгоритма алгоритма ДПФ с прореживанием по времени для 8-точечного ДПФ имеет вид:
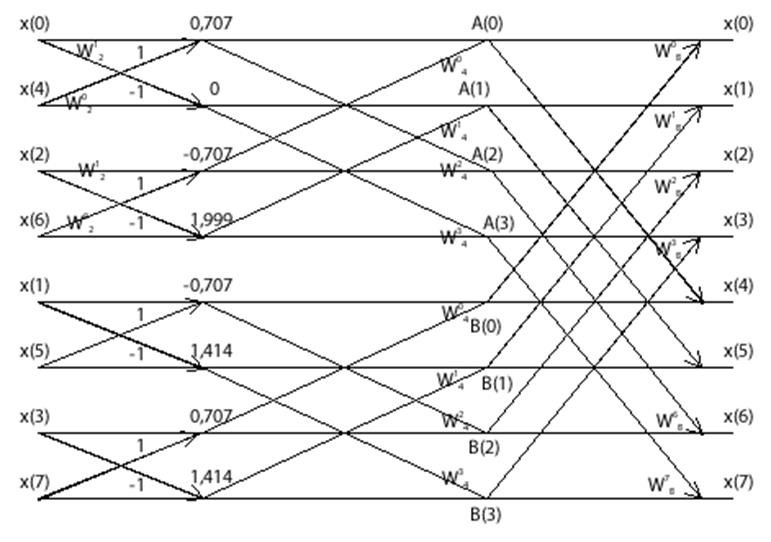
Рисунок 2
![]()
Выходные
значение первого каскада даны на рисунке и очевидны, т.к.
![]()
Выходные данные второго каскада
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Вычисляя результат третьего каскада получаем
окончательный ответ:
Вычисляя результат третьего каскада получаем
окончательный ответ:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Результат получился аналогичным задаче 6, что позволяет утверждать, что БПФ не является аппроксимацией ДПФ, а представляет собой ДПФ с уменьшенным количеством арифметических операций.
Задачи к разделу 10
Задача 1 Необходимо спроектировать КИХ-фильтр нижних частот со следующими ограничениями
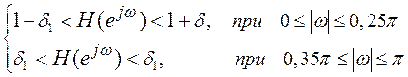
Для этого применяем окно ![]() к импульсной характеристике
к импульсной характеристике ![]() идеального дискретного фильтра нижних
частот с частотой отсечки
идеального дискретного фильтра нижних
частот с частотой отсечки ![]() . Какое из стандартных
окон, перечисленных в подразделе 10,5 следует взять для достижения заданной
цели? Для каждого подшедшего окна необходимо уточнить длину M+1 требуемого
фильтра.
. Какое из стандартных
окон, перечисленных в подразделе 10,5 следует взять для достижения заданной
цели? Для каждого подшедшего окна необходимо уточнить длину M+1 требуемого
фильтра.
Решение:
В соответствии с условиями задачи АЧХ ФНЧ имеет вид:
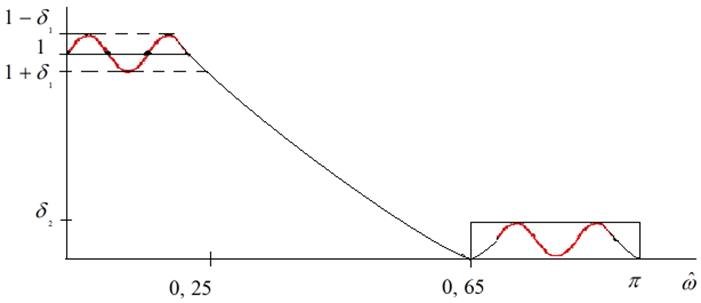
Допустимый уровень пульсаций
![]()
В соответствии с таблицей 10,2 подходят окна Хэннинга, Хэмминга и Блэкмана. При этом длина фильтров Хэннинга и Хэмминга определяется из равенств
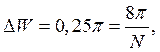 откуда N=32 и N+1=33
откуда N=32 и N+1=33
Для фильтра Блэкмана
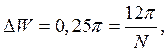 откуда N=48 и N+1=49
откуда N=48 и N+1=49
Задача 2 Необходимо спроектировать КИХ-фильтр нижних частот при следующих ограничениях
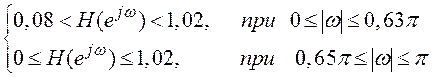
Для
этого применить окно Кайзера к импульсной характеристике ![]() идеального дискретного фильтра нижних
частот с частотой отсечки
идеального дискретного фильтра нижних
частот с частотой отсечки ![]() . Найти параметры
. Найти параметры ![]() и N окна Кайзера,
при которых выполняются заданные ограничения.
и N окна Кайзера,
при которых выполняются заданные ограничения.
Решение:
В соответствии с п.10.5.1.
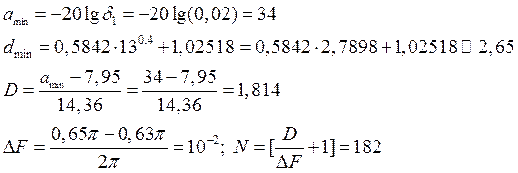
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.