Другие предметы \ Основы цифровой обработки сигналов

Практикум по курсу "Основы цифровой обработки сигналов", страница 2

Система устойчива, поскольку реакция – сумма конечного числа входных воздействий, линейна, поскольку описывается линейным оператором  и стационарна, поскольку сдвиг воздействия по времени не влияет на число суммируемых воздействий

1) 

2) 

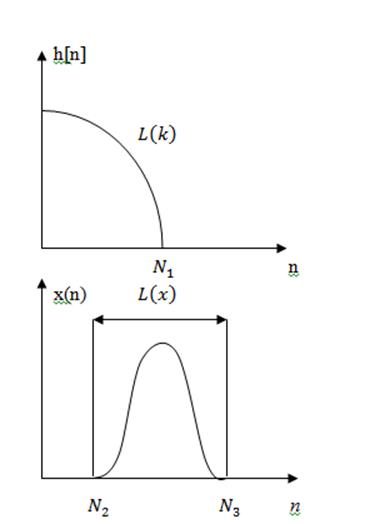
Задача 2. Известно, что длительность импульсной характеристики  линейной стационарной системы равна . Кроме того, ненулевые отсчеты входного воздействия  распложены в промежутке . Как следствие, реакция системы равна нулю всюду, кроме некоторого интервала . Необходимо выразить  и  через , и .

Ответ: (реакция не может быть раньше воздействие)

Задача 3. Линейная дискретная система описывается разностным уравнением:

Необходимо найти:

1)  Передаточную функцию;

2)  Импульсную характеристику системы.

Ответ:

1) 

2) 

Решение:

1)  Используя формулу для ПФ, выраженной через внутренние параметры ЛДС (коэффициенты РУ):

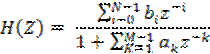
Получим

Полюсы этой системы равны , т.е. система неустойчива.

2) 

Где α*k  - простой к-й полюс (вещ. или мнимое число)

Ak –  коэффициент разложения при k-м полюсе (константа)

М-1 – количество полюсов

Разложив на простейшие множители знаменатель дроби исходном соотношением для H(Z), получим

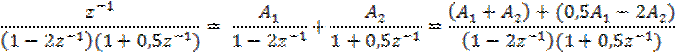
Откуда

, то имеем

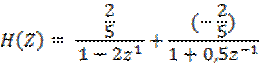
Поскольку импульсная характеристика – это реакция ДДС на единичный импульс U0 (n), который выражается через свёртку импульсной характеристики и единичного импульса, а в Z – плоскости свёртке во временной области соответствует произведение Z-изображения (теорема о свёртке) ПФ U0 (n), имеем

, т.к.

оригинал ПФ (суть ИХ) во временной области (см. табл. соответств.)

     (*)

Для проверки правильности нахождения импульсной характеристики, перепишем РУ в виде

и решим его методом прямой подстановки при нулевых начальных условиях.

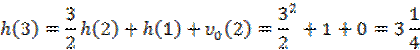
и т.д.

аналогичные вычисления по формуле (*) дают следующие идентичные результаты

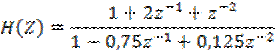
Задача 4 Получить расчетные формулы для АЧХ и ФЧХ на основе передаточной функции  звена 2 порядка

Решение:

Выполним следующие преобразования

– заменим и перейдем к частной характеристике

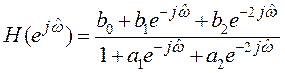
– разложим экспоненты:

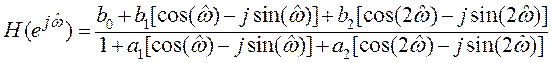
– выделим вещественные и мнимые части в числителе и знаменателе

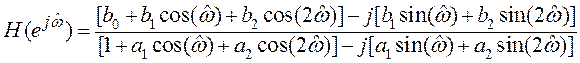
– запишем АЧХ и ФЧХ, исходя из их определений:

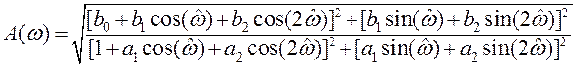
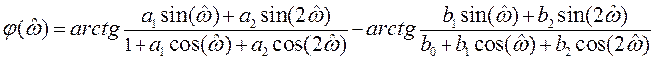
Задача 5 Дана нуль-полюсная диаграмма КИХ-фильтра 1-го порядка (рис. 1). Вывести выражение для АЧХ, используя формулу (П.2.9)

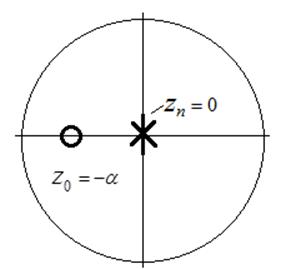
Рисунок 1.

Решение:

Применительно к КИХ-фильтру 1-го порядка формула (п.2.9.) принимает следующий вид:

, где  - расстояние от точки на окружности с угловой координатой Ф до точки расположение нуля (рисунок 2).

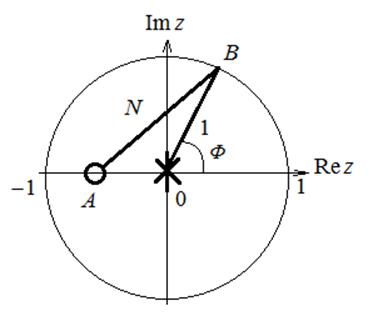
Рисунок 2.

В треугольнике АОВ выразим длину стороны АВ=N через длины двух других сторон:

.

В подкоренном выражении фигурируют длины, поэтому  надо брать по модулю. Подставляя в это выражение , получим

Задача 6.1. Найти АЧХ и ФЧХ ЛДС по известной передаточной функции

Решение:

Произведем замену переменной , тогда ЧХ

Откуда АЧХ

и ФЧХ

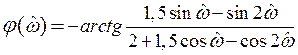
Задача 6.2. Пусть ПФ ЛДС 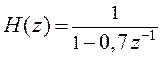, найти ее АЧХ и ФЧХ

Решение:

Для КЧХ запишем

Откуда АЧХ и ФЧХ

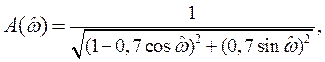
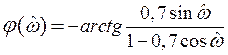
Задача 6.3. Пусть на ЛДС с передаточной функцией  воздействует дискретная синусоида ,  . Найти реакцию ЛДС в установившемся режиме.

Решение:

В соответствии с условием задачи

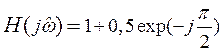
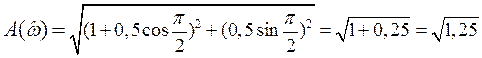
Тогда для установившегося режима получаем реакцию (т.к. )

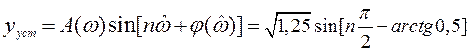
Задачи к разделу 7

Задача 1 Построить структуру прямой канонической 1й,2й и 3й формы для данной ПФ

a) 

Данной ПФ соответствует система РУ:

υ(n)=x(n)+0,75υ(n-1)-0,125υ(n-2)

y(n)=υ(n)+2υ(n-1)+υ(n-2)

z-1
 

z-2
 

y(n)
 

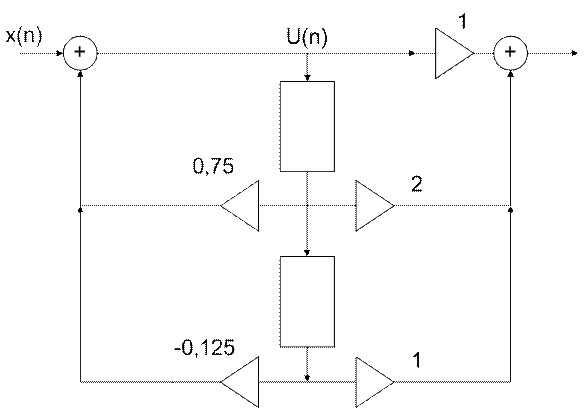
Рис.1 Структура прямой канонической формы 1

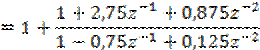
Данной ПФ соответствует система РУ

y(n)=box(n)+(b1-bob1)υ(n-1)+(b2-boa2)υ(n-2)=x(n)+(2+0,75)υ(n-1)+(1-0,125)υ(n-2)= =x(n)+2,75υ(n-1)+0,875υ(n-2)

Скачать файл