υ(n)=x(n)-a1υ(n-1)-a2υ(n-2)=x(n)+0,75υ(n-1)-0,125 υ(n-2)
|
|
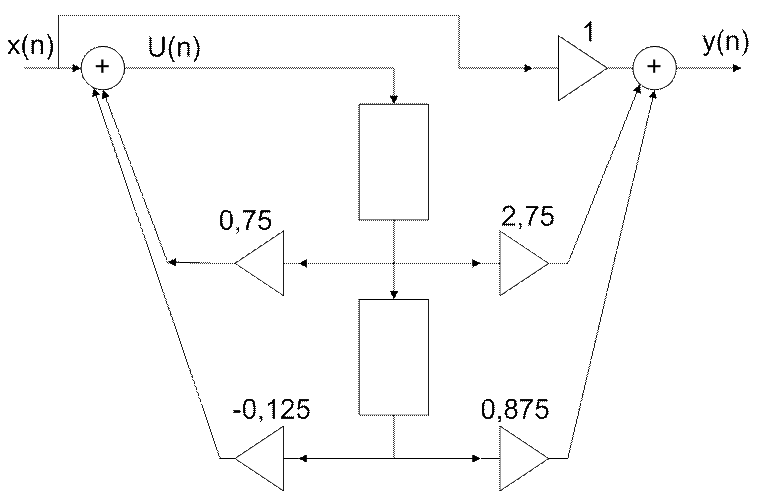
Рис.2 Структура прямой канонической формы 2
ПФ и система РУ для прямой канонической формы 3 имеют вид:
![]()
![]()
![]()
![]()
![]()
y(n) = x(n) + υ1(n-1)
υ1(n) = 2x(n) + 0,75y(n) + υ2(n-1)
υ2(n) = x(n) – 0,125y(n)
|
|
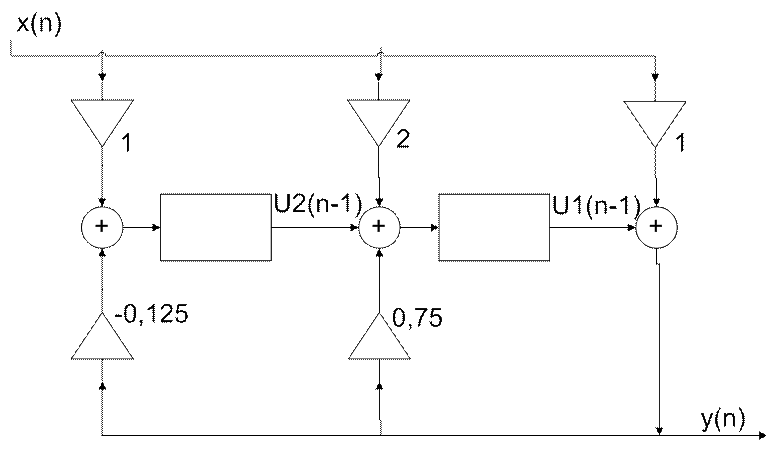
Рис.3 Прямая каноническая форма 3
Практикум к разделу 8
Задача 1. Определить ДПФ каждой из перечисленных конечных последовательностей, считая, что все они имеют длину N, где N-чётно а) x(n) = б(n); б) x(n) = б (n-n0), где 0≤n0≤N-1;
в)
x(n) = ![]()
г)
x(n) = ![]()
Решение:
а)
![]()
б)
![]()
в) ![]()
Δn=2
Воспользуемся известным соотношением
![]() ,
,
Откуда
![]()
г)
![]()
ДПФ определяем как сумму членов конечной геометрической прогрессии

Откуда

Задача
2.
Дано: ![]() , i=0,1,…,7. Требуется произвести
дискретное преобразование Фурье.
, i=0,1,…,7. Требуется произвести
дискретное преобразование Фурье.
Решение: Пусть ![]() , тогда
, тогда

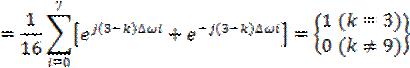
Задача
3.
Было произведено быстрое преобразование Фурье для ряда из 512 значений (![]() ), подвергшихся выборке с частотой 1 кГц. Какова
частота самой высокой гармоники сигнала, которую можно проанализировать?
), подвергшихся выборке с частотой 1 кГц. Какова
частота самой высокой гармоники сигнала, которую можно проанализировать?
Решение: Самая высокая гармоника сигнала, которую можно проанализировать, равна ½ частоты выборки, то есть 500 Гц. С интервалом 1 мс было выбрано 512 значений, поэтому период первой гармоники равен 0,512 с, а её частота равна 1,95 Гц.
![]()
Задача 4. Осуществить начальную перестановку разрядов для алгоритма БПФ с прореживанием по времени, если количество данных равно 16.
Решение :
|
Исходный сигнал |
Прореженный сигнал |
||
|
Десятичная система |
Двоичная система |
Двоичная система |
Десятичная система |
|
0 |
0000 |
0000 |
0 |
|
1 |
0001 |
1000 |
8 |
|
2 |
0010 |
0100 |
4 |
|
3 |
0011 |
1100 |
12 |
|
4 |
0100 |
0010 |
2 |
|
5 |
0101 |
1010 |
10 |
|
6 |
0110 |
0110 |
6 |
|
7 |
0111 |
1110 |
14 |
|
8 |
1000 |
0001 |
1 |
|
9 |
1001 |
1001 |
9 |
|
10 |
1010 |
0101 |
5 |
|
11 |
1011 |
1101 |
13 |
|
12 |
1100 |
0011 |
3 |
|
13 |
1101 |
1011 |
11 |
|
14 |
1110 |
0111 |
7 |
|
15 |
1111 |
1111 |
15 |
Задача
5.
Пусть непрерывный периодический сигнал с периодом T=1мс (![]() c) имеет вид ряда Фурье
c) имеет вид ряда Фурье
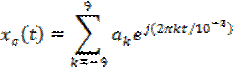
В
результате дискретизации сигнала с шагом ![]() получится последовательность
получится последовательность ![]() , т.е.
, т.е. ![]()
Вопросы:
а)
является ли последовательность ![]() периодической и каков её период;
периодической и каков её период;
б) достаточно ли мал шаг дискретизации, чтобы обеспечить отсутствие искажений аналогового сигнала;
в)
выразить коэффициент ДПФ последовательности ![]() через ак.
через ак.
Решение: а)
![]() периодична, поскольку исходный аналоговый сигнал
периодичен. Т.к. период период дискретизации в 6 раз меньше периода аналогового
сигнала, в одном его периоде будет взято 6 значений , т.е. период дискретной
последовательности N=6.
периодична, поскольку исходный аналоговый сигнал
периодичен. Т.к. период период дискретизации в 6 раз меньше периода аналогового
сигнала, в одном его периоде будет взято 6 значений , т.е. период дискретной
последовательности N=6.
б)
максимальная частота в аналоговом сигнале ![]() , в то время как частота дискретизации
, в то время как частота дискретизации ![]() . Условия теории Котельникова
. Условия теории Котельникова ![]() не соблюдается, следовательно восстановить исходный
сигнал по дискретному без искажений невозможно.
не соблюдается, следовательно восстановить исходный
сигнал по дискретному без искажений невозможно.
в) представим

Тогда
ДПФ ![]()
![]()

Воспользуемся известным соотношением

Т.е.
показатель экспоненты должен быть кратен ![]() , откуда справедливо соотношение
, откуда справедливо соотношение
![]()
Оно соблюдается в следующих случаях
![]()
![]()
![]()
Соответственно
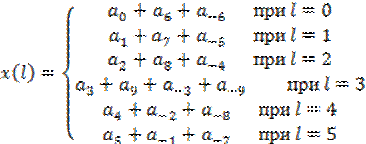
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.