Обобщенная схема ЦОС. Дискретизация аналогового сигнала. Основная полоса частот. Описание линейных дискретных систем в частотной области. Понятие частотной характеристики (ЧХ). Связь ЧХ с передаточной функцией. Алгоритм быстрого преобразования Фурье с прореживанием по времени. Понятие о полиномах Чебышева, страница 3

Как и прежде, будем исходить из представления частотной характеристики в виде

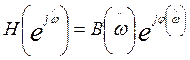, где амплитудная функция всегда положительна в полосе пропускания, но может принимать как положительные, так и отрицательные значения в полосе задерживания, при этом для АЧХ по определению амплитудной функции справедливы соотношения

Поскольку коэффициенты  передаточной функции КИХ-фильтров с линейной ФЧХ обладают определенной симметрией, достаточно знать лишь половину требуемых коэффициентов синтезируемого фильтра.

Амплитудную функцию частоты удобно представить в форме тригонометрического полинома 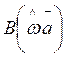, например для фильтра чётного порядка с симметричными коэффициентами (см. разд.10)

 (11.1)

где  - вектор коэффициентов, связывающий амплитудную и передаточную функции соотношением

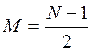 - порядок полинома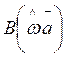

Если известны коэффициенты , нетрудно записать передаточную функцию

;

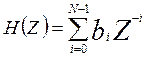Таким образом, задача оптимального синтеза состоит в определении такого вектора коэффициентов а полинома 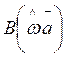, при котором достигается минимальный порядок передаточной функции.

11.1.1.1  Формулировка задачи

Для определенности рассмотрим фильтр НЧ, требование к амплитудной функции  которого изображены на рисунке 11.1. Област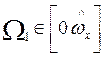и  и , в которых заданы требования к АЧХ будем называть к интервалам аппроксимации не относятся, поскольку в них требование к АЧХ не задается.

Рисунок 11.1

Таким образом, в данном случае формулировка задачи состоит в следующем. Необходимо найти полином вида (11.1) минимального порядка М_min,  для которого выполняются условия

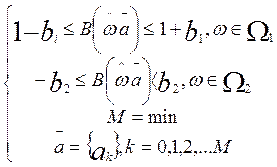, (11.2)

В этом случае целевой функцией (оптимизируемым параметром является порядок М_min  полинома 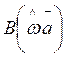, или же число коэффициентов передаточной функции. При этом необходимо определить сам вектор коэффициентов . В такой формулировке решение задачи на сегодняшний день неизвестно. Однако задачу (11.2) можно заменить многократным решением другой, более простой задачи, если поступить следующим образом:

-  зафиксировать порядок М (или число коэффициентов N ПФ), т.е. целевую функцию перевести в параметр

-  перевести отклонение b в целевую функцию

-  найти вектор коэффициентов , обеспечивающий минимум максимального отклонения

-  проверить, удовлетворяет ли полученное решение заданным требованиям к АЧХ.

За некоторое число этапов при последовательном уменьшении или увеличении параметра М (или N) обязательно найдется ………………… b не ………………….требований к АЧХ).

Система соотношений (11.2)……………. приведена к виду

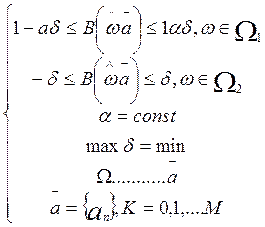
где постоянная a определяет очевидные соотношения между и  и называется весовым коэффициентом ().

11.1.1.2  Процедура решения задачи оптимального синтеза.

Процедура решения сводится к следующему:

1.  из практических соображений или по эмпирическим формулам задается начальное значение М=М_1, имеющее смысл первого приближения.

2.  при назначенном порядке выполняется первая итерация (первый этап), результатом вычислений которой является величина .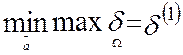

3.  полученное значение  сравнивается попарно с допустимыми значениями отклонений в полосах пропускания и задержания (. Возможны два результата сравнения и в соответствии с ними дальнейшие варианты действий.

Если требования к АЧХ удовлетворены, тогда можно попытаться уменьшить М_1; при новом М₂<М₁ выполнить вторую итерацию задачи (17.3) и получить новое значение 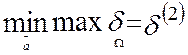; которое будет больше предыдущего, т.е. : проверить выполнение заданных требований. Известно, что за конечное число подобных итераций обязательно найдется такое минимальное значение М_min=M_opt, при котором еще выполняются условия задачи, на этом процедура заканчивается.

Если требования к АЧХ не удовлетворены, тогда необходимо увеличить М₁ и при новом М₂>М₁ решить задачу (17.3); получив , вновь проверить выполнение заданных требований и, если они не выполняются, увеличить М_2. Как и в предыдущем случае найдется (за конечное число подобных итераций) такое минимальное значение М_min=M_opt, при котором выполняются условия задачи; на этом процедура заканчивается.