12 СИНТЕЗ БИХ-фильтров
Методика синтеза частотно-избирательных БИХ-фильтров (НЧ, ВЧ, ПФ, РФ) базируются на хорошо развитом аппарате расчета аналоговых фильтров и преобразована передаточной функции аналогового фильтра в передаточную функцию цифрового фильтра. Аналоговый фильтр, рассчитанный по требованиям, заданным к цифровому фильтру называется фильтром-прототипом, или просто «прототипом». При решении задачи синтеза фильтр обычно бывает, задан АЧХ или ЧХ этого фильтра. Наиболее просто задача синтеза ЦФ решается в том случае, если известна ЧХ аналогового фильтра-прототипа. Метод синтеза ЦФ, основанный на использовании данной характеристики, называют методом инвариантности импульсной характеристики.
12.1 Синтез БИХ-фильтров методом инвариантности импульсной характеристики (метод стандартного Z-преобразования)
Рассматриваемый метод является исторически одним из первых методов синтеза БИХ-фильтров, использующих непосредственную дискретизацию аналогового фильтра. Метод вытекает из естественного желания получить такой цифровой фильтр, импульсная характеристика которого h(n) хорошо моделирует непрерывную импульсную характеристику g(t) аналогового фильтра-прототипа.
12.1.1 Постановка задачи и ее решение.
Пусть задана частота дискретизации 
, а, следовательно, и период дискретизации
Т цифрового фильтра.
ОПРЕДИЛЕНИЕ
Под инвариантностью импульсной характеристики понимается равенство отсчетов ЧХ цифрового фильтра h(n) значениям отсчетов ЧХ аналогового фильтра, взятым с периодом дискретизации Т.
Для синтезирования такого ЦФ необходимо найти ИХ прототипа g(t).
- получить ЧХ БИХ-фильтра h(nT) путем дискретизации g(t) c периодом Т (рис. 18.1)
Рисунок 12.1.
Решение.
Пусть известна передаточная функция устойчивого аналогового фильтра-прототипа G(p) (p-оператор
Лапласа 
; для устойчивости 
),
имеющая М полюсов Pxi (i – номер полюса, i=1,2,
…,М). найдем ЧХ g(t), для чего представим функцию G(р)
в виде суммы простых дробей (в предположении, что степень числителя не
превосходит степень знаменателя) (см. ……)
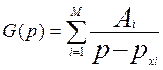, (12.1)
где Аi – коэффициент разложения при i-м полюсе. Коэффициент разложения может быть как вещественным, так и комплексным в зависимости от того, является ли i-й полюс вещественным или комплексным. В последнем случае, как полюсы, так и соответствующие им коэффициенты разложения могут встречаться лишь сопряженными парами. Коэффициенты разложения могут быть найдены по формуле
Как известно, импульсная характеристика прототипа является обратным преобразованием Лапласа передаточной функции
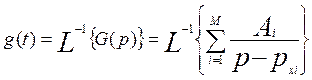
Откуда по свойству линейности преобразования Лапласа имеем
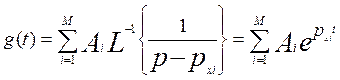
Дискретизируя g(t) с периодом Т (это и есть непосредственная дискретизация аналогового фильтра), получаем импульсную характеристику синтезируемого БИХ-фильтра.
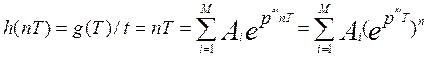, (12.2)
Найдем передаточную функцию БИХ-фильтра
(12.3)
Выражение (12.3) в общем случае, как это было отмечено ранее, содержит комплексные коэффициенты. Для перехода к передаточной функции с вещественными коэффициентами необходимо попарно сложить дроби, имеющие комплексно сопряженные полюсы, в результате чего получим М/2 звеньев второго порядка с вещественными коэффициентами.
, (12.4)
При обозначениях
, 
Нетрудно установить связь между коэффициентами простых дробей и звена (…….).
; 
;
; 
Из (12.3) и (12.4) получаем искомую передаточную функцию БИХ-фильтра, ЧХ которого инвариантна импульсной характеристике аналогового прототипа
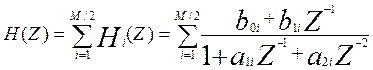, (12.5)
При выводе (12.5) предполагалось, что полюсы 
комплексные, в случае же вещественного
полюса 
цифровой фильтр будет иметь также
вещественный полюс 
, которому соответствует звено
1-го порядка вида
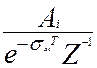, (12.6)
с вещественным коэффициентом разложения.
Нечетное количество полюсов М означает, что имеется хотя бы один вещественный полюс. Тогда соответствующее ему звено 1-го порядка (12.6) надо вынести за знак суммы, после чего верхний предел суммирования определить как (М-1)/2.
Передаточной функции (12.5) соответствует параллельная структура фильтра (рис. 12.1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.