Обобщенная схема ЦОС. Дискретизация аналогового сигнала. Основная полоса частот. Описание линейных дискретных систем в частотной области. Понятие частотной характеристики (ЧХ). Связь ЧХ с передаточной функцией. Алгоритм быстрого преобразования Фурье с прореживанием по времени. Понятие о полиномах Чебышева, страница 6

Рисунок 12.1.

12.2  Синтез БИХ-фильтров методом билинейного Z-преобразования.

12.2.1  Определение билинейного преобразования.

Воспользуемся соотношением и выразим комплексный оператор p через комплексную переменную Z, что позволит представить…………

Представим luZ в виде ряда Тейлора.

Взяв первый член этого ряда, получим

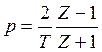, (12.7)

Перейдем к отрицательным системам переменной Z путем умножения числителя и знаменателя на , что даст при обозначении  даст

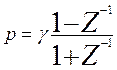, (12.8)

Обратная зависимость Z от p имеет вид

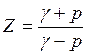, (12.9)

Передаточная функция цифрового фильтра H(Z)  получается из передаточной функции аналогового фильтра G(p) заменяем p на Z согласно (12.8), т.е.

 

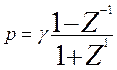
Преобразование (12.8) представляем собой дробно-рациональную функцию первого порядка от  и называется билинейным Z-преобразованием.

12.2.2  Свойства билинейного Z-преобразования.

Билинейное Z-преобразование обеспечивает однозначное отображение p-плоскости на Z-плоскость а) частотная ось  однозначно отображается в единую окружность. Действительно, единичная окружность описывается равенством , а оператор  для частотной оси имеет вид , поскольку . Тогда из (12.9) получаем

,

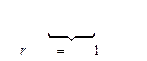
т.е. имеем единичную окружность. Рассмотрим, каким образом отображается положительная и отрицательная области частотной оси на Z-плоскость, для чего определим аргумент Z.

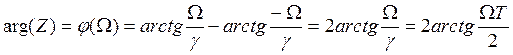
Рассмотрим отображение некоторых точек  на Z-плоскость.

; ; ; ; ; ; ; ;

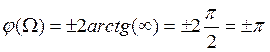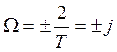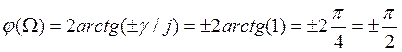Полученные соответствия указаны на рисунке 12.2.

Рисунок 12.2 Отображение p-плоскости на Z-плоскость…….

Продолжая подобные вычисления, можно убедиться, что ось  однозначно отображается в единичную окружность на Z-плоскости, причем положительная ось частотной оси  отображается на верхнюю, а отрицательная область – на нижнюю полуокружность.

1. Левая полуокружность однозначно отображается внутрь единичного круга, а правая полуплоскость - вне его.

Для доказательства этого утверждения достаточно знать, в каких пределах лежат значения радиуса r. Воспользуемся выражением (12.9), куда подставим оператор , и исследуем  при положительных и отрицательных значениях .

Числитель подкоренного выражения при , что соответствует левой p-полуплоскости, оказывается меньше знаменателя, поэтому r>1 и левая полуплоскость отображается внутрь единичного круга Z-плоскости. При , что соответствует правой полуплоскости, числитель оказывается больше знаменателя, поэтому r>1 и правая полуплоскость отображается на всю Z-плоскость вне единичного круга.

2. Цифровой фильтр устойчив, если устойчив его аналоговый прототип, поскольку полосы последнего лежали в левой полуплоскости, отображаемой внутрь единичного круга Z-плоскости

3. соотношение между аналоговыми  и цифровыми частотами принципиально нелинейно, т.е. шкала деформируется из (12.7) при  и , поскольку рассматривается только частотная ось и единичная окружность, можно получить (см. н/о)

, (12.10)

(12.11)

Полученной нелинейностью преображать нельзя, поэтому в процессе синтеза фильтра необходимо пересчитывать частоты из цифровой области в аналоговую и наоборот. При этом восстановление цифровых частот происходит автоматически, поскольку оно заложено в формуле (12.9).

4. В цифровой области сохраняются свойства оптимальности АЧХ аналогового прототипа вследствие однозначности отображения частотной оси в единичную окружность, что исключает эффект наложения, характерный для метода интервальности импульсной характеристики.

5. Порядок цифрового фильтра равен порядку аналогового прототипа, т.е. количество их полюсов одинаково. Количество нулей ЦФ совпадает с количеством нулей прототипа, учитывая и нуль прототипа по бесконечности .

Пример

Передаточная функция прототипа.

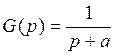
имеет полюс  и нуль . Для получения H(Z) произведем в G(p) замену (12.8)

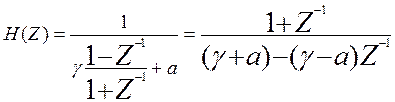
Видно, что H(Z) имеет один ожидаемый полюс

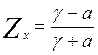
Согласно формуле (12.8) и появился один вещественный нуль , соответствующий нулю , поскольку при билинейном преобразовании  отображается в точку Z=-1.