В рассматриваемом примере в передаточной функции аналога-прототипа (п.1) необходимо пересчитать два параметра w0 и Dw, или связанные с ними ¦0 и D¦. На практике их удобно выражать через два других параметра, а именно: через границы полосы пропускания на уровне 0,7, т.е. через частоты среза:
; 
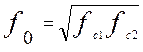, (п.3)
Представленные соотношения тем точнее, чем больше добротность. При добротности Q³4 погрешность менее 1%. Обозначим через ¦с1 и ¦с2 границы полосы пропускания непредыскаженного аналога-прототипа. Построив график аналога-прототипа для ¦0 = 10 кГц и Q=4, можем получить ¦с1 =8,75 кГц; ¦с2 = 11,25 кГц; D¦ = 2,5 кГц.
Найдем значения ¦с1 и ¦с2 с использованием формулы пересчета (п.2), которую в нашем случае перепишем в виде
,
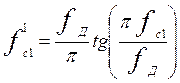(п.4)
Примем значение частоты дискретизации 
= 50 кГц.
Подстановка и найденных ранее ¦с1 и ¦с2 дает
для 
и 
следующие
значения: =9,96 кГц, =13,85
кГц.
Если подставив эти значения вместо ¦с1 и ¦с2 в формулы (п.3), то для предыскаженного аналога-прототипа получим следующее значение параметров,
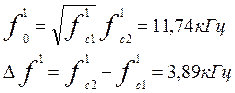
Представив эти значения в соотношении (п.1), получим выражение для передаточной функции предыскаженного аналога-прототипа:
, (п.5).
Примерный вид АЧХ исходного аналога-прототипа и его
предыскаженной версии показан на рис. П.1
1 – АЧХ аналога-прототипа
2 – АЧХ предыскаженного аналога-прототипа
3-
АЧХ цифрового БИХ-фильтра для 
= 50
кГц
Рисунок П.1
Подставим в формулу (п.5) соотношение
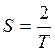
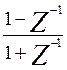
и для принятых числовых значений параметров получим выражение для передаточной функции искомого цифрового фильтра:
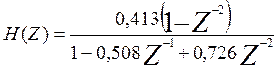, (п.6)
Обратим внимание на то, передаточная функция, рассчитанная предыдущим методом имела нуль первого порядка.
В передаточной функции (п.6) присутствуют два нуля. Появление второго нуля в передаточной функции БИХ-фильтра, рассчитанного методом билинейного Z-преобразования, вполне закономерно, поскольку при билинейном преобразовании точка S=¥ отображается в точку Z=-1 (доп. нуль).
На рисунке П.1 показана нормированная АЧХ, построенная по соотношению (п.6).
В заключении хочется отметить, что а) метод билинейного Z-преобразования пригоден в тех случаях, когда требования АЧХ фильтра-прототипа задаются ступенчатой функцией частоты, что свойственно частотно-избирательным фильтрам (НЧ, ВЧ, ПФ, РФ);
б) не пригоден для синтеза корректирующих фильтров (фильтров с произвольными АЧХ), фильтров с линейной ФЧХ, поскольку ни ФЧХ ни ЧХ из-за нелинейности преобразования не сохраняется.
Таким образом, когда, что касается практического применения методов, то в тех случаях, когда АЧХ рассчитываемого фильтра предъявляются повышенные требования к точности воспроизведения во всем частотном диапазоне, целесообразно применять методы стандартного Z-преобразования. В остальных случаях, когда АЧХ фильтра задается лишь ограниченным набором параметров, более предпочтителен метод билинейного Z-преобразования, поскольку он полностью подключает эффект наложения и не требует увеличения частоты дискретизации для уменьшения ошибок, вызванных этим явлением.
11 CИНТЕЗ ОПТИМАЛЬНЫХ (ПО ЧЕБЫШЕВУ)
КИХ-фильтров
Среди достаточного разнообразия методов синтеза КИХ-фильтров с линейной ФЧХ широкое применение получил «классический» метод оптимального (по Чебышеву) синтеза, который при обеспечении заданных допустимых отклонениях d1 и d2 АЧХ от 1 и 0 соответственно позволяет получить передаточную функцию фильтра наименьшего порядка удовлетворяющую заданным требованиям и ограничениям. Такие фильтры относят к классу оптимальных.
11.1 Понятие об оптимальном (по Чебышеву) синтезе фильтров
Конструирование передаточной функции минимального порядка, при котором обеспечивается выполнение всех заданных требований и ограничений означает, что в результате решения поставленной задачи достигается:
- необходимая точность аппроксимации заданной характеристики согласно выбранному критерию близости;
- выполнение устойчивых ограничений (вид ФЧХ, физическая реализуемость и т.п.)
Такая задача называется задачей оптимального синтеза.
11.1.1 Постановка задачи оптимального синтеза.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.