С4.
В правильной четырехугольной пирамиде
SABCс
вершиной в точке Sна
продолжении ребра SAза
точкой А взята точка М так, что расстояние от точки М до
плоскости SCD равно 24. Найти АМ, если АВ = 16, sin![]() = 0,6, где
= 0,6, где ![]() – угол
наклона боковой грани к плоскости основания пирамиды.
– угол
наклона боковой грани к плоскости основания пирамиды.
С5.
Около прямой четырехугольной призмы
описан цилиндр. Основание призмы – прямоугольник, диагонали которого образуют
угол ![]() , а расстояние между боковым ребром призмы и
скрещивающейся с ним диагональю основания равно
, а расстояние между боковым ребром призмы и
скрещивающейся с ним диагональю основания равно ![]() . Найти площадь боковой поверхности призмы,
если объем цилиндра равен
. Найти площадь боковой поверхности призмы,
если объем цилиндра равен ![]() .
.
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ
Контрольная работа №1
Часть I
A1. Использовать свойства степени с действительным показателем.
A2. Использовать свойства корней.
A3. Использовать формулу сокращенного умножения: суммы кубов.
A4. Использовать теорему Виета.
A5. Числитель и знаменатель дроби разложить на множители,
используя метод группировки, и использовать формулу ![]() .
.
A6. Решить методом интервалов. На числовой оси отметить точки –1, 5,определить знак дроби в каждом из полученных интервалов и выбрать те промежутки, где дробь меньше либо равна нулю.
A7. Возвести обе части уравнения в куб.
A8. Использовать метод интервалов.
A9. Дискриминант должен быть отрицательным.
A10. Возвести обе части уравнения в квадрат, решить и сделать отбор значений согласно области определения уравнения.
Часть II
B1. Разложить числа на простые множители и найти НОК и НОД, затем ответить на поставленный вопрос в задаче.
B2. Записать в виде степени с дробным показателем, перемножить степени с одинаковым основанием и привести подобные.
B3. Приравнять сухую массу цемента на складе и в привезенной смеси.
B4. Выделить полный квадрат сначала под вторым квадратным корнем, затем – под первым.
B5. Применить формулу разности квадратов, затем – разности кубов.
B6. Использовать свойства корней и формулу ![]()
B7. Если система двух линейных уравнений с двумя
неизвестными не имеет решений, то 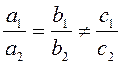 , где
, где ![]() – коэффициенты при неизвестных, а
– коэффициенты при неизвестных, а ![]() – свободные члены.
– свободные члены.
B8. Если система двух линейных уравнений с двумя
неизвестными имеет бесчисленное множество решений, то 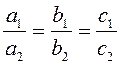 ,
где
,
где ![]() – коэффициенты при неизвестных, а
– коэффициенты при неизвестных, а ![]() – свободные члены.
– свободные члены.
B9. Квадратный трехчлен принимает только положительные
значения, следовательно, 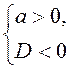 .
.
B10. Квадратное уравнение имеет два корня разных знаков,
значит, 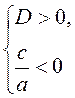 .
.
B11. Умножить обе части второго уравнения на 3 и сложить уравнения системы.
B12. Из условия задачи видно, что ![]() является
решением, учесть это и поделить обе части уравнения на
является
решением, учесть это и поделить обе части уравнения на ![]() ,
раскрыть куб разности и решить квадратное уравнение.
,
раскрыть куб разности и решить квадратное уравнение.
B13. Уравнение имеет положительные корни, следовательно, 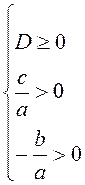 .
.
B14. Сделать замену переменной 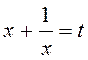 .
.
B15. Перемножить первый и четвертый, второй и третий
сомножители и сделать замену переменной ![]() .
.
B16. Найти производную, критические точки, промежутки монотонности, знаки функции на концах этих промежутков.
B17. Решение задачи аналогичное решению задачи №16.
B18. Раскрыть модуль и решить систему квадратных неравенств.
B19. Найти область определения и возвести в квадрат обе части неравенства.
B20. Записать уравнение параболы в виде ![]() и учесть условие.
и учесть условие.
B21. Возвести в квадрат обе части уравнения.
B22. Все собрать в левую часть неравенства, привести к общему знаменателю и решить методом интервалов.
B23. Использовать формулы общего члена и суммы n членов арифметической прогрессии.
B24. Перемножить степени с одинаковым основанием и применить формулу суммы бесконечно убывающей геометрической прогрессии.
B25. Применить характеристическое свойство арифметической и геометрической прогрессий.
Часть III
C1. Использовать область определения неравенства и знаки дроби.
C2. Использовать теорему Виета и условие существования действительных и различных корней квадратного уравнения.
C3. Использовать определение модуля действительного числа.
C4. Использовать определение модуля действительного числа и знак арифметического корня.
C5. Приравнять функции и сделать замену переменной ![]() .
.
Часть I
A1. Использовать формулу синуса двойного угла.
A2. Использовать формулы приведения.
A3. Воспользоваться формулой корней тригонометрического уравнения, содержащего функцию синуса.
A4. Воспользоваться замечанием ![]() .
.
A5. Применить формулы сложения.
A6. Множество значений функции ![]() есть
отрезок
есть
отрезок ![]() , учесть параллельный перенос графика.
, учесть параллельный перенос графика.
A7. Воспользоваться формулой корней тригонометрического уравнения, содержащего функцию косинуса.
A8. Применить формулы сложения и тригонометрическое тождество.
A9. Воспользоваться формулой корней тригонометрического уравнения, содержащего функцию тангенса.
A10. Используя тригонометрическую единицу, перейти к квадратному уравнению относительно функции синуса и решить его.
Часть II
B1. Использовать свойство периодичности функции синуса и формулы приведения.
B2. Применить формулы выражения синуса и косинуса половинного аргумента через косинус целого.
B3. Найти тангенс данного аргумента, затем косинус.
B4. Применить формулу синуса двойного угла, поделить на ![]() , решить уравнение и выбрать корни из
заданного интервала.
, решить уравнение и выбрать корни из
заданного интервала.
B5. Воспользоваться формулами приведения и тригонометрическими тождествами.
B6. Ввести новую переменную, решить уравнение, выбрать x, принадлежащие заданному отрезку.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.