Контрольная работа по математике №4, 11 класс
Решения заданий части А
А1. По основному логарифмическому тождеству ![]() . В итоге исходное выражение примет вид:
. В итоге исходное выражение примет вид: ![]() . Ответ
№2.
. Ответ
№2.
А2. 1) Упростим заданное уравнение: 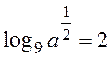 , тогда, по свойству логарифма:
, тогда, по свойству логарифма: 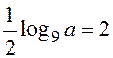
![]()
![]() . 2)
. 2)
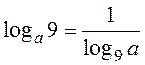 =
=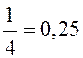 . Ответ
№1.
. Ответ
№1.
 А3. Область определения
А3. Область определения ![]() .
Упростим исходную функцию:
.
Упростим исходную функцию: ![]() . По свойству
логарифмической функции:
. По свойству
логарифмической функции:![]() . Умножим все части
неравенства на 2 и прибавим по 9:
. Умножим все части
неравенства на 2 и прибавим по 9: ![]() ,
, ![]() . Значит,
. Значит, ![]() . Ответ
№3. А4. Исходное уравнение является тождеством, следовательно, х принимает
любые значения из области допустимых значений. Находим ОДЗ:
. Ответ
№3. А4. Исходное уравнение является тождеством, следовательно, х принимает
любые значения из области допустимых значений. Находим ОДЗ: ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Графически решим неравенство
. Графически решим неравенство ![]() и получим, что
и получим, что ![]() (см.
рис.). Целые числа в этом промежутке :
(см.
рис.). Целые числа в этом промежутке : ![]() , всего
5 чисел.
, всего
5 чисел.
Ответ №1.
А5.
Используем формулы: 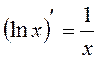 и
и 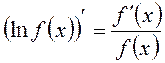 . Тогда
. Тогда
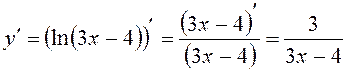 . Ответ
№1.
. Ответ
№1.
А6.
Используем формулу: ![]() . Тогда
. Тогда ![]()
![]()
![]()
![]()
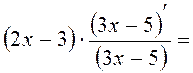
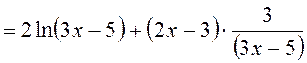 . При
. При ![]() получим
получим
![]()
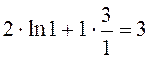 .
.
Ответ №3.
А7.
Чтобы найти угловой коэффициент
касательной в точке с абсциссой ![]() , нужно найти значение
производной заданной функции в этой точке. (Геометрический смысл производной):
, нужно найти значение
производной заданной функции в этой точке. (Геометрический смысл производной): ![]() ,
, ![]() .
.
Ответ №4.
А8.
Область определения заданной функции
описывается системой неравенств: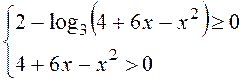 . Решаем первое
неравенство:
. Решаем первое
неравенство: ![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]() . Решим это неравенство
графически (см. рис. справа):
. Решим это неравенство
графически (см. рис. справа): ![]() .
.
 Решим
второе неравенство: Находим корни уравнения
Решим
второе неравенство: Находим корни уравнения ![]() :
: 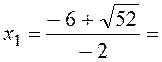
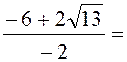
![]()
![]() Следовательно,
Следовательно, ![]() (см.
рис. слева). Общее решение системы:
(см.
рис. слева). Общее решение системы: ![]() . Теперь, по условию,
совмещаем этот промежуток с отрезком
. Теперь, по условию,
совмещаем этот промежуток с отрезком ![]() (см. рис. внизу) и
получаем искомые целые числа:
(см. рис. внизу) и
получаем искомые целые числа: ![]() . Их сумма равна 12.
. Их сумма равна 12.
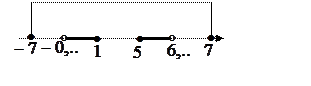 Ответ
№2.
Ответ
№2.
А9.
Упростим: 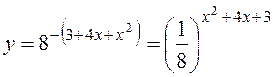 и
произведем замену:
и
произведем замену: 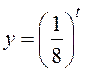 ,
, ![]() .
Теперь нужно определить, какие значения принимает функция t. Графиком этой функции является парабола, ветви ее направлены
вверх, а вершина находится в точке
.
Теперь нужно определить, какие значения принимает функция t. Графиком этой функции является парабола, ветви ее направлены
вверх, а вершина находится в точке ![]() (
(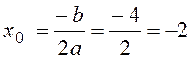 ,
, ![]() ). Следовательно,
). Следовательно,
![]() . Возвращаемся к искомой функции
. Возвращаемся к искомой функции 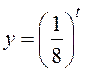 , которая является монотонно убывающей. Если
, которая является монотонно убывающей. Если
![]() , то
, то ![]() . Если
. Если ![]() , то
, то ![]() .
Значит,
.
Значит, ![]() .
.
Ответ №3.
А10.
Функция 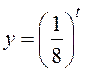 является
монотонно убывающей, (так как
является
монотонно убывающей, (так как 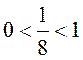 ), следовательно,
), следовательно, ![]() . Решим это неравенство:
. Решим это неравенство: ![]()
![]()
![]()
![]()
![]() . Ответ
№2.
. Ответ
№2.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.