Указания к решению задач контрольных работ № 1-5 по курсу "Математика" (Использовать свойства степени с действительным показателем. Использовать область определения неравенства и знаки дроби), страница 5

В12. Поверхность тетраэдра состоит из 4-х правильных треугольников со стороной, равной диагонали грани куба.

В13. Угол между скрещивающимися прямыми равен углу между пересекающимися прямыми, которые параллельны данным. Найти диагональ боковой грани, используя заданный угол, и применить теорему Пифагора, чтобы найти высоту параллелепипеда.

В14. Искомый угол между апофемой и отрезком – радиусом окружности вписанной в основание.

В15. Треугольник, заданный тремя точками сферы, – прямоугольный. Центр окружности описанной около прямоугольного треугольника лежит на середине гипотенузы.

В16. В равнобедренной трапеции, диагонали которой взаимно перпендикулярны, высота равна полусумме оснований.

В17. Сечение является ромбом, одна диагональ которого равна диагонали основания, другая – диагональ куба.

В18. В основании пирамиды – прямоугольный треугольник, высота пирамиды равна радиусу окружности, описанной около этого треугольника.

В19. Высота пирамиды равна катету треугольника, лежащего в основании.

В20. Осевое сечение конуса равносторонний треугольник. Радиус сферы равен радиусу окружности, описанной около этого треугольника.

В21. Высота пирамиды равна высоте прямоугольного треугольника, проведенной к гипотенузе. Площадь этого треугольника известна.

В22. Аналогично B21.

В23. Высота сечения равна половине бокового ребра пирамиды. Обозначить сторону основания пирамиды за а и решить задачу в общем виде, затем подставить значение а.

В24. Обозначить стороны основания параллелепипеда а и b. Двумя способами записать объем пирамиды, образованной сечением и вершиной нижнего основания, не лежащей в плоскости сечения.

В25. Обозначить сторону основания пирамиды за а, вычислить тангенс искомого угла.

Часть III

С1. Сечение является пятиугольником. Площадь сечения равна сумме площадей треугольника и трапеции.

С2. Одно из ребер основания является проекцией бокового ребра призмы на плоскость основания. Одна из боковых граней является прямоугольником.

С3. Сечение является параллелограммом, площадь которого равна удвоенной площади одного из треугольников, на которые диагональ параллелепипеда разбивает сечение. Диагональ параллелепипеда примем за основание треугольника, т.к. точки В и фиксированы. Площадь сечения будет наименьшей, если высота треугольника будет наименьшей. Задача сводится к нахождению отношения, в котором основание общего перпендикуляра двух скрещивающихся прямых (диагонали параллелепипеда и не пересекающегося с ней бокового ребра) делит это боковое ребро. При решении использовать подобие  прямоугольных треугольников.

С4. Прямая МА пересекает плоскость SCD в точкеS. Расстояние от точки М до заданной плоскости пропорционально расстоянию от точки А до этой плоскости. Для нахождения бокового ребра пирамиды использовать теорему Пифагора и синус заданного угла наклона боковой грани к плоскости основания пирамиды.

С5. Диагональ прямоугольника является диаметром цилиндра. Угол между диагоналями прямоугольника равен , следовательно, треугольник, образованный одной из сторон основания призмы и половинами диагоналей, является правильным. Расстояние между скрещивающимися прямыми равно высоте этого правильного треугольника.

ИТОГОВЫЕ ТЕСТЫ (для самоконтроля)

Решить, проверить решения по ответам на стр. 40

Тест № 1

(Записать номер полученного ответа)

1. Упростить .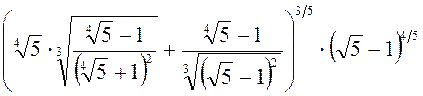

1)          2)                3)                4)                   5)

2. Упростить   .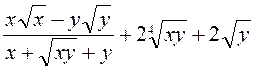

1)        2)        3)        4)        5)

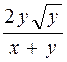
3. Найти количество целых значений параметра а, при которых абсцисса и ордината вершины параболы  отрицательны.

1) 8                       2) 4                       3) 5                       4) 6                       5) 7

4. Найти сумму корней уравнения .

1) 0,5                    2) –16,5                3) 11,5                  4) 8                       5) 12,5