Указания к решению задач контрольных работ № 1-5 по курсу "Математика" (Использовать свойства степени с действительным показателем. Использовать область определения неравенства и знаки дроби), страница 4

B8. Освободиться от знака логарифма и решить квадратное уравнение.

B9. Применить тождество .

B10. Преобразовать уравнение по свойствам логарифмов и сделать замену .

B11. Прологарифмировать обе части уравнения по основанию 0,25 и сделать замену переменной.

B12. Все степени, входящие в уравнение, записать в виде степеней, основания которых – простые числа.

B13. Сначала решить уравнение, не содержащее параметр, учесть область определения и условие задачи.

B14. Применить свойства логарифмов.

B15. Последовательно освободиться от логарифма, учитывая допустимые значения и монотонность функции.

B16. Сделать замену переменной .

B17. Учесть область определения, множитель  опустить, учитывая, что  является решением неравенства и решить неравенство .

B18. Данное неравенство заменить двумя системами.

B19. Найти производную дроби и вычислить производную в заданной точке.

B20. Найти производную, критические точки, значение функции в точках максимума и минимума и ответить на главный вопрос задачи.

B21. Записать уравнение касательной, в уравнение подставить координаты точки (–3; 4). По теореме Виета найти сумму абсцисс точек касания.

B22. Найти производную, приравнять ее тангенсу угла наклона касательной к положительному направлению оси Ох, найти угол.

B23. Использовать условие перпендикулярности прямых:

B24. Найти критические точки, определить знаки производной в полученных интервалах, определить точки экстремума функции.

B25. Найти производную, критические точки; выбрать только те, которые принадлежат заданному отрезку. Найти значения функции в критических точках и на концах отрезка.

Часть III

C1. Первое уравнение упростить по определению логарифма, во втором использовать свойства логарифмов.

C2. Использовать свойства логарифмов, ввести новую переменную  и рассмотреть решение неравенства при c> 1 и 0 < c< 1.

C3. Найти область определения обеих функций и определить условие, при котором области пересекаются.

C4. Решить систему .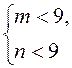

C5. Выяснить, сколько корней может иметь каждое из этих уравнений и решить первое уравнение при найденном значении р.

Контрольная работа №5

Часть I

А1. Вспомнить взаимное расположение в пространстве двух плоскостей.

А2. Вспомнить взаимное расположение прямой и плоскости.

А3. Вспомнить признак перпендикулярности прямой и плоскости.

А4. Использовать свойство перпендикулярных плоскостей и признак перпендикулярности прямой и плоскости.

А5. Использовать теорему Пифагора.

А6. Использовать формулу для вычисления длины окружности и объема конуса.

А7. Найти высоту правильной четырехугольной пирамиды.

А8. Поверхность правильного тетраэдра состоит из четырех правильных треугольников.

А9. Использовать теорему Пифагора.

А10. Использовать формулу для вычисления объема шара и площади сферы.

Часть II

В1. Использовать формулу для вычисления полной поверхности призмы.

В2. Вспомнить соотношение между диагональю куба и его стороной.

В3. Радиус окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.

В4. Используя площадь основания, найти сторону основания. Из площади сечения найти высоту.

В5. Площади подобных фигур относятся как квадраты их линейных размеров.

В6. Радиус шара равен радиусу окружности, вписанной в треугольник – осевое сечение конуса.

В7. Высота цилиндра равна длине окружности основания.

В8. Обозначить сторону основания за а, рассмотреть треугольник, содержащий угол  и найти высоту этого треугольника по теореме синусов. Затем найти синус искомого угла.

В9. Использовать теорему Пифагора.

В10. Составить три уравнения: на площадь каждого диагонального сечения и на теорему Пифагора, т. к. диагонали ромба взаимно перпендикулярны. Решить полученную систему.

В11. Радиус второго сечения равен радиусу шара. Радиус шара найти по теореме Пифагора.