ВВЕДЕНИЕ
Сборник лабораторных работ содержит описание экспериментальных задач, выполняемых студентами, обучающимися по специальности "Инженерная теплофизика", при изучении курса "Физика плазмы".
Лабораторный практикум включает в себя три работы. Каждая из работ подразумевает четырехчасовое аудиторное выполнение и последующую обработку результатов с применением ЭВМ.
Студенты, успешно прошедшие практикум, получают навыки экспериментальной работы с различными источниками низкотемпературной плазмы и современной диагностической аппаратурой, получают представление о спектральных и зондовых методах измерения параметров равновесной и неравновесной низкотемпературной плазмы в магнитном поле, а также глубже усваивают теоретические методы, служащие основой экспериментального изучения плазмы.
Авторы выражают глубокую признательность О.А. Синкевичу и А.М. Семенову за консультации при постановке лабораторных работ и за любезно предоставленную возможность использовать подготовленные ими методические материалы; В.А. Кондратьевой и М.Н. Рудавиной, без помощи которых эти работы не были бы реализованы, а также В.Ф. Чиннову за внимательное отношение к рукописи данного сборника, приведшее к существенному улучшению изложения работ лабораторного практикума.
ЛАБОРАТОРНАЯ РАБОТА № 1
ОПРЕДЕЛЕНИЕ РАДИАЛЬНОГО ПРОФИЛЯ ТЕМПЕРАТУРЫ
В ПЛАЗМЕ ДУГОВОГО РАЗРЯДА
1.1. Методические основы эксперимента.
1.1.1. Механизмы излучения плазмы.
Излучение плазмы существенно отличается от излучения твердого тела. Если спектр излучения твердого тела – непрерывная кривая, подчиняющаяся закону Планка, то спектр плазмы представляет собой комбинацию дискретной и непрерывной составляющих.
Дискретный (линейчатый) спектр плазмы обусловлен связанно-связанными переходами и обсуждается в ЛР № 3. Непрерывный спектр обусловлен двумя механизмами: свободно-свободными и свободно-связанными переходами электронов.
Свободно-свободные переходы электронов имеют место при торможении свободных электронов в поле заряженных (и нейтральных) частиц плазмы. Этот процесс сопровождается электромагнитным излучением, которое называется тормозным. Свободно-связанные переходы электронов представляют собой рекомбинацию электронов и положительных ионов; если освобождающаяся при этом энергия уносится в виде кванта излучения, то такой процесс называют фоторекомбинацией, а само излучение – рекомбинационным.
Можно показать [1], что кванты с длиной волны l, удовлетворяющей условию ![]() , излучаются в основном
рекомбинационным механизмом, в противном случае – тормозным. Следовательно, в
дуговой плазме с температурой
, излучаются в основном
рекомбинационным механизмом, в противном случае – тормозным. Следовательно, в
дуговой плазме с температурой ![]() К излучение в видимом
диапазоне (
К излучение в видимом
диапазоне (![]() мкм) обусловлено главным образом
фоторекомбинационными процессами.
мкм) обусловлено главным образом
фоторекомбинационными процессами.
1.1.2. Излучение оптически тонких сред и уравнение Абеля.
Уравнение переноса излучения в среде, поглощение которой пренебрежимо мало (так называемый оптически тонкий слой), может быть записано в виде
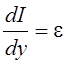 , (1.1)
, (1.1)
где
I – интенсивность излучения (энергия, проходящая в
единицу времени через единичную площадку в единичном телесном угле в
направлении оси y), ![]() – объемный коэффициент
излучения (энергия, излучаемая единичным объемом плазмы в единицу времени в
направлении оси y в единицу телесного угла). Объемный коэффициент
излучения является функцией температуры плазмы и излучаемой длины волны.
– объемный коэффициент
излучения (энергия, излучаемая единичным объемом плазмы в единицу времени в
направлении оси y в единицу телесного угла). Объемный коэффициент
излучения является функцией температуры плазмы и излучаемой длины волны.
Во многих случаях (и в данной лабораторной работе) дуга горит в цилиндрическом канале специального устройства – плазмотрона. Стенки канала охлаждаются, поэтому температура плазмы сильно неоднородна по радиусу канала, изменяясь от значения ~104 К на оси до комнатных температур (в широком смысле) на стенке канала. Поэтому объемный коэффициент излучения также неоднороден по радиусу канала.
Рассмотрим интенсивность излучения цилиндрического плазменного столба в направлении оси y (рис. 1.1). В этом случае в уравнении (1.1) интенсивность излучения будет функцией x и y, объемный коэффициент – функцией радиуса r. Интенсивность излучения, выходящего из плазменного столба вдоль оси y при заданной координате x, можно найти интегрированием уравнения (1.1) по y:
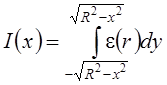 (1.2)
(1.2)
Производя замену переменной интегрирования, (1.2) можно привести к виду
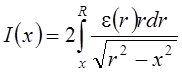 . (1.3)
. (1.3)
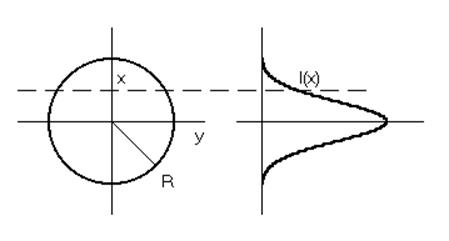
Рис. 1.1. Сечение столба дуги и распределение интенсивности излучения.
В уравнении (1.3) интенсивность излучения измеряется непосредственно в эксперименте, объемный коэффициент является искомой величиной. Следовательно, (1.3) представляет собой интегральное уравнение для определения e (оно называется уравнением Абеля).
Уравнение (1.3) можно решить (см.[2]):
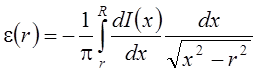 (1.4)
(1.4)
Можно
получить аналитическое выражение для ![]() , аппроксимируя функцию
, аппроксимируя функцию ![]() , например, полиномами от x2.
, например, полиномами от x2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.