Рис. 2.3. Экспериментальная зависимость отношения холловской составляющей электрического поля к продольной составляющей, в зависимости
от напряженности магнитного поля при P=0.6 мм рт. ст.
Комплекс Ω, стоящий в правой части соотношения (3) часто называется параметр Холла. Эффект Холла в данном случае проявляется в возникновении внутри трубки, за счет разделения пространственного заряда в плазме, поперечной (холловской, вдоль оси y) составляющей электрического поля. Если бы стенки отсутствовали, то в направлении y был бы зафиксирован электрический ток, называемый холловским током, несмотря на то, что внешним источником электрического потенциала создается только продольное (вдоль оси x) электрическое поле.
Нарушение линейности зависимости Ey/Ex от Bz при большой напряженности магнитного поля,
фиксируемое в эксперименте, следует объяснить, в первую очередь, сказывающимся
воздействием амперовой силы 
на плазму с током. В
результате, столб разряда, в зависимости от направления внешнего магнитного
поля, смещается вдоль оси y и прижимается к боковой поверхности трубки, что
приводит к существенным искажениям геометрии и параметров разряда.
Воспользовавшись экспериментальным графиком зависимости Ey/Ex от Bz , следует определить тангенс угла наклона кривой в окрестности точки Bz=0 и из выражения (2.3) определить τ – время потери импульса электронами при столкновениях с тяжелыми частицами. По полученному значению τ далее следует получить значение температуры электронов Te, которое можно определить из уравнения энергии для электронной компоненты плазмы.
В случае, когда учитываются только упругие потери, данное уравнение может быть получено исходя из следующих предположений. Все омические потери в объеме равны σE2, где E2=Ex2+Ey2 . С другой стороны, они равны количеству энергии, которое в течение одной секунды находящиеся в единице объема плазмы ne электронов, каждый из которых в единицу времени испытывает 1/τ столкновений, передают тяжелым частицам (атомам и ионам). Уравнение баланса энергии, в таком случае, выглядит следующим образом:
.
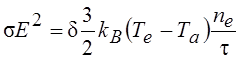Здесь δ=2me /ma – доля энергии, передаваемой при упругом столкновении от электрона к тяжелой частице; Ta – температура тяжелых частиц, для газоразрядной плазмы ее, с хорошим приближением, можно считать равной комнатной температуре. После простейших преобразований из данного уравнения получаем
.
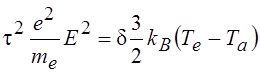(2.4)
2.5. Определение времени потери импульса по измерению напряженности электрического поля в разряде пониженного давления (при горении разряда в режиме Шоттки).
После того, как по наклону экспериментального графика Ey/Exопределеновремя потери импульса τ, а по уравнению энергии (2.4) найдено значение электронной температуры Te, их следует сравнить со значениями, полученными по методике, применяемой для расчета параметров газового разряда, горящего в т.н. режиме Шоттки.
Данный режим горения разряда характеризуется тем, что при пониженных давлениях механизм гибели электронов в плазме радикально меняется. В плотной плазме основным механизмом их гибели является т.н. трехчастичная объемная рекомбинация, т.е. реакция вида e- + e- + i+ ↔ e- + A. В разряженной же среде объемная рекомбинация мала по сравнению с уходом заряженных частиц на стенку под действием амбиполярной диффузии. В этом режиме суммарное электрическое поле E в разряде и температура электронов Teопределяется только произведением Pd, где P – давление в разрядной трубке; d – диаметр трубки, для данной установки d=30 мм. Методика расчета зависимостей E (Pd) и Te (Pd) детально изложена в [3] и здесь не приводится.
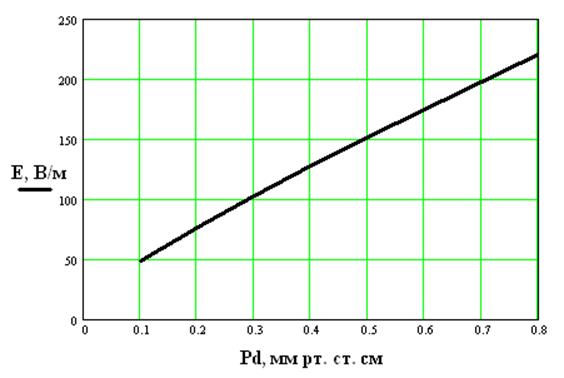
Зависимость E от параметра Pdдля разряда в аргоне приведена на рис. 2.4. В Таблице 2.2 та же зависимость дана численно. По известному значению d и определенному в ходе эксперимента значению P по рис.2.4 или с помощью Таблицы. 2.2 следует найти теоретическое значение напряженности электрического поля E для разряда, горящего в режиме Шоттки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.