Лабораторный практикум по курсу "Физика плазмы" (Лабораторные работы № 1-3. Определение радиального профиля температуры в плазме дугового разряда. Определение температуры дуговой плазмы методом относительных интенсивностей), страница 9

7.  Анализ погрешности измерения времени потери импульса и определения электронной температуры.

2.8. Контрольные вопросы

1.  Объяснить, какую траекторию, при отсутствии столкновений, имеют заряженные частицы: А) в однородном электрическом; Б) в однородном магнитном; В) в однородных электрическом и магнитном полях, когда они  перпендикулярны друг другу.

2.  Объяснить возникновение эффекта Холла.

3.  Объяснить, что представляет собой параметр Холла и проанализировать влияние давления на его величину.

4.  Объяснить причины различия между напряжением зажигания и напряжением горения газового разряда.

ЛАБОРТОРНАЯ РАБОТА № 3

ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ ДУГОВОЙ ПЛАЗМЫ

МЕТОДОМ ОТНОСИТЕЛЬНЫХ ИНТЕНСИВНОСТЕЙ

3.1. Методические основы эксперимента.

3.1.1. Метод относительных интенсивностей для определения температуры дуги.

Плазма излучает как в непрерывном спектре, так и в дискретном. Излучение в дискретном спектре обусловлено переходами возбужденного атома или иона с энергией уровня E_m в менее возбужденное состояние с энергией E_n, в результате чего излучается квант энергии 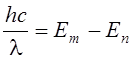. Энергия, излучаемая единичным объемом плазмы в единицу времени на длине волны l, вычисляется по формуле

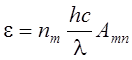,                                                         (3.1)

где  – концентрация возбужденных атомов на уровне m, [см^–3];  – вероятность перехода , [с^–1]. Вероятности перехода являются индивидуальными характеристиками атомов и ионов, и для многих веществ они определены (экспериментально либо теоретически). Вероятности некоторых переходов атомов аргона, а также статистические веса и энергии верхних уровней приведены в таблице 3.1.

Таблица 3.1

Характеристики некоторых переходов атомов аргона

Помимо таблицы 3.1, справочные данные, необходимые для выполнения работы, содержатся в справочном разделе программы, предлагаемой для выполнения вычислений, также в [5-7].

В случае равновесной плазмы концентрация частиц имеет больцмановское распределение по уровням энергии,

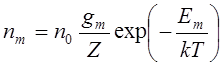,                                                    (3.2)

где  – суммарная концентрация частиц,  – статистический вес уровня m, Z – статистическая сумма.

Метод относительных интенсивностей определения температуры равновесной плазмы (например, дуговой) основан на совместном использовании (3.1) и (3.2) для двух излучаемых плазмой линий. Подставляя (3.2) в (3.1), находим для линий с длинами волн  и :

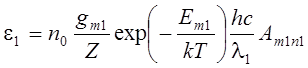,                                      (3.3)

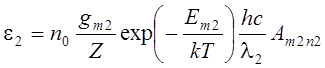,                                   (3.4)

Входящая в (3.3), (3.4) концентрация  обычно неизвестна, статистическую сумму также довольно трудно вычислить. Однако если взять отношение (3.3) и (3.4),

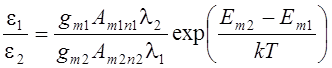,                                  (3.5)