Определение линейного коэффициента ослабления интенсивности коллимированного пучка γ-квантов

1.  Цель работы

Определить линейный коэффициент ослабления интенсивности коллимированного пучка γ-квантов.

2.  Закон ослабления интенсивности коллимированного пучка γ-квантов

При прохождении через вещество мононаправленных γ-квантов происходит ослабление их потока в результате актов поглощения (фотоэффект, образование электронно-позитронных пар) или рассеяния (эффект Комптона).

Интенсивность φ моноэнергетического мононаправленного γ-излучения определяют по соотношению:

,          (7.1)

где Е_γ – энергия γ-кванта, МэВ; N_γ – плотность потока γ-квантов, γ – кв/(см^2.с).

Значение N_γ равно числу γ-квантов, проходящих за 1 с через площадку в 1 см² , которая ориентирована перпендикулярно направлению их распространения.

Узкий мононаправленный пучок образуется путем коллимирования диафрагмами 2 потока γ-квантов, излучаемых источником И (рис. 7.1). Если источник моноэнергетический, то детектор 3 регистрирует γ-кванты одинаковой энергии, не испытавшие взаимодействия с исследуемым образцом 1 толщиной х. Поэтому для регистрации γ-квантов в геометрии узкого пучка можно использовать гейгеровский счетчик.

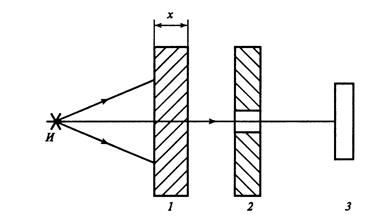
Рис. 7.1. Геометрия узкого пучка γ-квантов

В случае однократного взаимодействия уменьшение интенсивности dφ при прохождении слоя dx пропорционально толщине этого слоя и значению φ:

,          (7.2)

где μ – линейный коэффициент ослабления, см^-1.

Перейдем от дифференциальной к интегральной форме закона ослабления:

,          (7.3)

где φ₀ и φ(x) – соответственно, интенсивности пучка, входящего (х = 0) в слой вещества и выходящего из него.

Экспоненциальный множитель в правой части представляет вероятность прохождения толщины х без взаимодействия. Согласно закону ослабления в случае моноэнергетического источника зависимость  от x является прямой, выходящей из начала координат. Ее угол наклона определяется значением μ. Используя определение эффективности регистрации γ-излучения счетчиком Гейгера, получим для скорости счета n [имп/мин] соотношение, аналогичное предыдущему:

,          (7.4)

Закон ослабления в таком виде  используется для определения μ в геометрии узкого пучка, приведенной на рис. 7.1:

.          (7.5)

Характеристикой проникающей способности γ-квантов является толщина Δ_1/2 слоя половинного ослабления, необходимая для снижения вдвое интенсивности узкого пучка. Подставив условие  или  в (7.3) или (7.4), соответственно, получим:

.          (7.6)

При возрастании Е_γ увеличивается проникающая способность γ-излучения. Наиболее эффективным защитным материалом является свинец, имеющий минимальные значения Δ_1/2.

Второй характеристикой проникающей способности излучения является средний свободный пробег γ-кванта в веществе, который обратно пропорционален линейному коэффициенту ослабления μ.

Отнесение результатов взаимодействия не к единице объема вещества, а к единице его массы соответствует переходу от линейного к массовому коэффициенту ослабления μ_m:

,          (7.7)

где ρ – плотность вещества, г/см³.

Введение μ_m приводит к необходимости использования массовой толщины х [г/см²]:

.          (7.8)

Согласно размерности х_m, эта величина соответствует толщине материала с площадью основания в 1 см², содержащей 1 г вещества.

При теоретическом рассмотрении взаимодействия γ-излучения с веществом его результаты относят к одному атому (эффекты поглощения) или электрону (эффект Комптона), вводя атомный μ_а и электронный μ_е коэффициенты ослабления:

;  ,          (7.9)

где n_а, n_е – соответственно атомная [ат/см³] и электронная [эл/см³] плотность вещества.

Значения n_а, n_е находятся по соотношению:

,          (7.10)

где N_A – число Авогадро, А – атомная масса, Z – атомный номер вещества.

3.  Процессы взаимодействия γ-квантов с веществом

Поток γ-квантов при прохождении через защиту ослабляется вследствие трех независимых процессов: фотоэффекта, эффекта Комптона и эффекта образования пар, следовательно:

,          (7.11)

где τ, σ, χ – соответствующие линейные коэффициенты взаимодействий.

а) Фотоэффект – поглощение γ-кванта связанным электроном, входящим в состав одной из оболочек атома. Не существует однозначной взаимосвязи между направлением распространения γ-кванта и углом вылета фотоэлектрона. Вероятность процесса уменьшается при возрастании разности между энергией γ-кванта Е_γ и энергией связи электрона с ядром на К-, L-оболочках (Е_K, Е_L). Следовательно, если Е_γ > Е_K, то основной вклад в общее поглощение на всех оболочках вносит фотоэффект на K-оболочке, в результате которого вырывается фотоэлектрон с кинетической энергией, равной разности Е_γ - Е_K. Поскольку для выполнения закона сохранения импульса в этом процессе необходима третья частица, поглощение γ-кванта свободным электроном невозможно.

Значение Е_K пропорционально Z² и равно 0,088 МэВ для свинца (Z = 82). Поэтому для большинства γ-излучателей выполняется условие Е_γ >> Е_K. Если при этом Е_γ не превышает энергию массы покоя электрона (m₀c² = 0,511 МэВ), то массовый коэффициент τ_m фотоэлектрического поглощения на K-оболочке вычисляют по формуле Гайтлера:

,          (7.12)

где α — относительная энергия γ-кванта, равная .

Согласно формуле Гайтлера вклад фотоэлектрического поглощения возрастает при увеличении Z и уменьшении Е_γ и является доминирующим при Е_γ < 0,05; 0,15; 0,5 МэВ для алюминия (Z = 13), меди (Z= 29) и свинца соответственно.

б) Эффект Комптона – рассеяние γ-кванта на свободном покоящемся электроне.

В результате рассеяния первичного γ-кванта с энергией Е_γ0 возникают рассеянный γ-квант с энергией Е_γs и комптоновский электрон отдачи с энергией Е_кэ.

В соответствии с законом сохранения энергии величина Е_кэ определяется как разность энергий первичного и рассеянного γ-квантов

.          (7.13)

Обозначив углы вылета рассеянного γ-кванта и электрона относительно направления распространения первичного γ-кванта θ и φ соответственно, запишем закон сохранения импульса в проекциях на оси х и у:

,          (7.14)