Гидродинамический подход. Приближение бесконечной проводимости, вмороженное магнитное поле

3.1.  Гидродинамический подход.

3.2.1.  Одножидкостная гидродинамика.

В рамках этой модели плазма рассматривается как проводящая жидкость. При этом в обычное гидродинамическое уравнение движения среды кроме силы, связанной с градиентом давления, вязкостью и т.д., добавляется пондеромоторная сила:

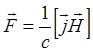                                                       (3.2.1)

где плотность тока,  напряженность магнитного поля.

Если пренебречь вязкостью и другими диссипативными силами, то уравнение движения проводящей жидкости имеет вид:

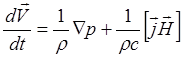                                            (3.2.2)

где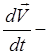ускорение рассматриваемого «элемента жидкости». Уравнение(3.2.2) написано в представлении Лагранжа, когда движение жидкости изучается путем слежения за траекторией выбранного элемента и, выписанная выше производная, является производной вдоль траектории; ее называют лагранжевой производной. Существует альтернативный подход, называемый представлением Эйлера, при котором рассматривается изменение скорости среды в выбранной точке пространства : эйлерова производная. Хотя она и является производной скорости по времени, но не имеет физического смысла ускорения. Связь между лагранжевой и эйлеровой  производными дается выражением:

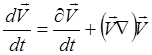
Поэтому уравнение (3.2.2) в представлении Эйлера будет выглядеть следующим образом:

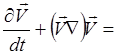
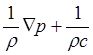
                            (3.2.2а)

Плотность тока задается законом Ома:

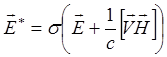                                     (3.2.3)

где напряженность электрического поля в системе отсчета, движущейся вместе с плазмой, проводимость плазмы, напряженность электрического поля в лабораторной системе координат.

Задание плотности тока с помощью закона Ома, при том, что проводимость плазмы считается константой - главный недостаток одно-жидкостной МГД теории. Во многих случаях этот подход неприменим, однако имеется достаточно много практически интересных случаев, когда такое упрощение является оправданным.

Система уравнений (3.2.2) – (3.2.3), описывающая движение плазмы, должна быть дополнена уравнениями Максвелла. Совместное их решение и составляет обсуждаемый подход к исследованию плазмы. Дополнительное существенное упрощение модели получается, если иметь в виду относительную медленность процессов, описываемых данным приближением, что позволяет пренебречь токами смещения. Тогда из всей системы уравнений Максвелла остается лишь:

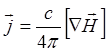                                                     (3.2.4)

и уравнение (3.2.2) принимает вид

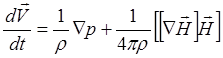                                          (3.2.5)

Используя известное соотношение векторного анализа:

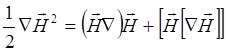                                         (3.2.6)

получим из него:

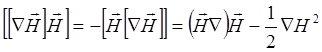                        (3.2.7)

и, подставив затем (3.2.7) в (3.2.5), имеем:

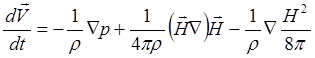                         (3.2.8)

Правая часть уравнения (3.2.8) содержит три члена, описывающие действие сил, связанных с градиентом давления, кривизной силовых линий и пространственным изменением модуля напряженности магнитного поля. Если магнитное поле меняется только в направлении, поперечном по отношению к силовым линиям, то второй член в правой части, связанный с кривизной силовых линий, обращается в нуль и уравнение может быть переписано в следующем виде:

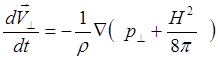                                           (3.2.9)

Здесь ускорение в направлении поперек силовых линий магнитного поля. Член входит в формулу на равных основаниях с газокинетическим давлением (поперечным) , поэтому его также можно интерпретировать как давление – давление магнитного поля. Таким образом, полученное выражение позволяет сделать практически важный вывод о возможности оказывать давление на плазму (проводящую среду) с помощью магнитного поля.

Приближение бесконечной проводимости, вмороженное магнитное поле.

Во многих случаях рассмотрение плазмы как проводящей жидкости может быть упрощено в еще большей степени: ее электрическое сопротивление устремляется к нулю. Это приближение называется приближением идеальной проводимости. В приближении идеальной проводимости электрическое поле в системе координат, связанной с плазмой, должно равняться нулю, ибо сколь угодно малое электрическое поле вызвало бы в идеальном проводнике бесконечно большой ток. Итак, полагаем  , что может быть переписано следующим образом:

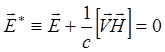                                                    (3.2.1)

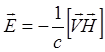                                                               (3.2.2)